Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho A và F ngồi ở hai đầu ghế
A. 48
B. 42
C. 46
D. 50
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 10 2017
Xem AF là một phần tử X, ta có 5!=120 cách xếp 5 người X;B;C;D;E.
Khi hoán vị A; F ta có thêm được một cách xếp.
Vậy có 2.120=240 cách xếp thỏa yêu cầu bài toán.
Chọn B.
CM
22 tháng 12 2018
số cách xếp 6 người vào 6 ghế là 6!.
Số cách xếp thỏa yêu cầu bài toán: 6!-240=480 cách.
Chọn A.
CM
20 tháng 10 2019
Đáp án D
Số cách xếp:
B C D E là 4! A và F là 2! ⇒ ∑ = 4 ! .2 ! = 48
CM
1 tháng 10 2019
Bước 1: Ta sử dụng tính chất riêng của hai bạn B và F trước. Hai bạn này chỉ ngồi đầu và ngồi cuối, hoán đổi cho nhau nên có 2! cách xếp.
Bước 2: Xếp vị trí cho các bạn còn lại, ta có cách xếp.
Vậy ta có 2!.5! = 240 cách xếp
Chọn C.
HT
27 tháng 12 2020
Eo ơi, đừng!! Tách ra đi bạn ơi, để thế này khủng bố mắt người đọc quá :(
Mà hình như mấy bài này có trong tập đề của thầy tui gởi nè :v
10 tháng 8 2018
a) giải cách này để bn dể hình dung nha :)
ta có : 2 người \(A;F\) ngồi cạnh nhau thì ta cứ tưởng tượng như lấy sợi dây buột 2 người này lại .
\(\Rightarrow\) ta có số cách để xếp \(A;F\) trên 6 vị trí là : \(2.\left(6-1\right)=10\)
và số cách xếp \(4\) người còn lại trên \(4\) vị trí còn lại là : \(A^4_4=4!=24\)
\(\Rightarrow\) số cách sắp xếp sao cho \(A\) và \(F\) ngồi cạnh nhau là \(10.24=240\) cách
b) ta có số cách sắp xếp \(6\) người ngồi trên \(6\) vị trí là \(A^6_6=6!=720\) cách
\(\Rightarrow\) số cách sắp xếp sao cho \(A\) và \(F\) không ngồi cạnh nhau là : \(720-240=480\) cách
vậy .....................................................................................................................
CM
15 tháng 7 2019
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có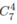 
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có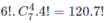 
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có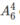 
cách.
Theo quy tắc nhân, có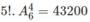 
cách.
a: Số cách xếp A, F ngồi ở hai ghế đầu là : 2!=2 cách.
Số cách xếp B;C;D;E vào bốn ghế còn lại là hoán vị của 4 phần tử nên có 4!=24 cách.
Số cách xếp thỏa yêu cầu bài toán: 2.24=48 cách.
Chọn A.