Biết lim x → 0 3 x 2 + 2 − 2 − 2 x x = a 2 b ( a b tối giản). Giá trị của a+b bằng:
A. − 1 2
B. 3
C. 1 2
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
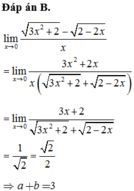
\(b\) hữu hạn nên \(x^2+ax+2=0\) có nghiệm \(x=1\)
\(\Rightarrow1+a+2=0\Rightarrow a=-3\)
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{x}-1}{x^2-3x+2}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(x-2\right)\left(\sqrt{x}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{1}{\left(x-2\right)\left(\sqrt{x}+1\right)}=-\dfrac{1}{2}\Rightarrow b=-\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(x+1\right)\sqrt{2x+1}}{\sqrt{5x^3+x+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(1+\dfrac{1}{x}\right)\sqrt{2+\dfrac{1}{x}}}{\sqrt{5+\dfrac{1}{x^2}+\dfrac{2}{x^3}}}=\sqrt{\dfrac{2}{5}}\)
Bạn coi lại, \(x\rightarrow-\infty\) hay \(+\infty\) nhỉ? (Dù a; b không đổi, vẫn là 2 và 5 nhưng \(x\rightarrow+\infty\) thì kết quả phải dương, ko có dấu trừ đằng trước)
AM
9 tháng 2 2022
a. \(lim_{x\rightarrow3}\dfrac{x^3-27}{3x^2-5x-2}=\dfrac{3^3-27}{3.3^2-5.3-2}=\dfrac{0}{10}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{x+2}-2}{4x^2-3x-2}=\dfrac{\sqrt{2+2}-2}{4.2^2-3.2-2}=\dfrac{0}{8}=0\)
c. \(lim_{x\rightarrow1}\dfrac{1-x^2}{x^2-5x+4}=lim_{x\rightarrow1}\dfrac{\left(1-x\right)\left(x+1\right)}{\left(x-1\right)\left(x-4\right)}=lim_{x\rightarrow1}\dfrac{-\left(x+1\right)}{x-4}=\dfrac{-\left(1+1\right)}{1-4}=\dfrac{2}{3}\)
d. Câu này mình chịu, nhìn đề hơi lạ so với bình thường hehe
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1
Giới hạn đã cho hữu hạn nên \(a=-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(b-x\right)^2-\left(x^2-6x+2\right)}{b-x+\sqrt{x^2-6x+2}}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(6-2b\right)x+b^2-2}{-x+\sqrt{x^2-6x+2}+b}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{6-2b+\dfrac{b^2-2}{x}}{-1-\sqrt{1-\dfrac{6}{x}+\dfrac{2}{x^2}}+\dfrac{b}{x}}=\dfrac{6-2b}{-2}=5\)
\(\Rightarrow b=8\)
Cả 4 đáp án đều sai, số lớn hơn là 8
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
\(\lim\limits_{x\rightarrow-3}\dfrac{x^2-1}{x+1}=\dfrac{\left(-3\right)^2-1}{-3+1}=-4\) (câu này \(x\rightarrow-3\) hay \(x\rightarrow-1\) vậy?)
\(\lim\limits_{x\rightarrow-2}\dfrac{4-x^2}{x+2}=\lim\limits_{x\rightarrow-2}\dfrac{\left(2-x\right)\left(x+2\right)}{x+2}=\lim\limits_{x\rightarrow-2}\left(2-x\right)=4\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1
\(=\lim\limits_{x\rightarrow0}\dfrac{2\left(\sqrt[]{2x+1}-1\right)+2-\sqrt[3]{x^2+x+8}}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{2.2x}{\sqrt[]{2x+1}+1}-\dfrac{x\left(x+1\right)}{\sqrt[3]{\left(x^2+x+8\right)^2}+2\sqrt[3]{x^2+x+8}+4}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{4}{\sqrt[]{2x+1}+1}-\dfrac{x+1}{\sqrt[3]{\left(x^2+x+8\right)^2}+2\sqrt[3]{x^2+x+8}+4}\right)\)
\(=\dfrac{23}{12}\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
Để giới hạn đã cho là hữu hạn thì \(a=1\)
\(\lim\limits_{x\rightarrow+\infty}\left(x+b-\sqrt{x^2-6x+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+2bx+b^2-\left(x^2-6x+2\right)}{x+b+\sqrt{x^2-6x+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2b+6\right)x+b^2-2}{x+b+\sqrt{x^2-6x+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{2b+6+\dfrac{b^2-2}{x}}{1+\dfrac{b}{x}+\sqrt{1-\dfrac{6}{x}+\dfrac{2}{x^2}}}=\dfrac{2b+6}{2}=b+3\)
\(\Rightarrow b+3=3\Rightarrow b=0\Rightarrow\left\{{}\begin{matrix}a=1\\b=0\end{matrix}\right.\)
HT
20 tháng 2 2021
a/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-x+1-x^2-x-1}{\sqrt{x^2-x+1}+\sqrt{x^2+x+1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-\dfrac{2x}{x}}{\sqrt{\dfrac{x^2}{x^2}-\dfrac{x}{x^2}+\dfrac{1}{x^2}}+\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}=-\dfrac{2}{1+1}=-1\)
b/ \(=\lim\limits_{x\rightarrow2}\dfrac{4x+1-9}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{4}{\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\dfrac{4}{\left(2+2\right)\left(\sqrt{4.2+1}+3\right)}=\dfrac{1}{6}\)
c/ \(=\lim\limits_{x\rightarrow-2}\dfrac{2x+5-1}{\left(x-2\right)\left(x+2\right)\left(\sqrt{2x+5}+1\right)}=\lim\limits_{x\rightarrow-2}\dfrac{2}{\left(x-2\right)\left(\sqrt{2x+5}+1\right)}=\dfrac{2}{\left(-2-2\right)\left(\sqrt[2]{2.\left(-2\right)+5}+1\right)}=\dfrac{2}{\left(-4\right).2}=-\dfrac{1}{4}\)
29 tháng 1 2023
a: \(=lim_{x->2}\dfrac{x^3-2x^2+4x^2-8x+2x-4}{-\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=lim_{x->2}\dfrac{\left(x-2\right)\left(x^2+4x+2\right)}{-\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=lim_{x->2}\dfrac{-x^2-4x-2}{x^2+2x+4}\)
\(=lim_{x->2}\dfrac{-1-\dfrac{4}{x}-\dfrac{2}{x^2}}{1+\dfrac{2}{x}+\dfrac{4}{x^2}}=\dfrac{-1}{1}=-1\)
b: \(lim_{x->2}\dfrac{x^3-2x^2+3x^2-6x+x-2}{\left(x-2\right)\left(x-1\right)}\)
\(=lim_{x->2}\dfrac{\left(x-2\right)\left(x^2+3x+1\right)}{\left(x-2\right)\left(x-1\right)}\)
\(=lim_{x->2}\dfrac{x^2+3x+1}{x-1}\)
\(=lim_{x->2}\dfrac{1+\dfrac{3}{x}+\dfrac{1}{x^2}}{\dfrac{1}{x}-\dfrac{1}{x^2}}\)
lim(1+3/x+1/x^2)=1>0
lim(1/x-1/x^2)=(x-1)/x^2<0
=>lim=dương vô cực