Cho đa thức P ( x ) = x 3 - 4 x 2 + 3 - 2 x 3 + x 2 + 10 x - 1
Tìm đa thức Q(x) biết P ( x ) + Q ( x ) = x 3 + x 2 + 2 x - 1
A. - 4 x 2 - 8 x - 3
B. 2 x 3 - 4 x 2 + 8 x - 3
C. 2 x 3 + 4 x 2 - 8 x - 3
D. 4 x 2 - 8 x - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B(3)=2*3^2-4*3+3=18-12+3=9
B(-1/2)=2*1/4-4*(-1/2)+3=1/2+3+2=1/2+5=11/2

Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b

a: Q(x)=3x^4+x^3+2x^2+x+1-2x^4+x^2-x+2
=x^4+x^2+3x^2+3
b: H(x)=2x^4-x^2+x-2-x^4+x^3-x^2+2
=x^4+x^3-2x^2+x
c: R(x)=2x^3+x^2+1+2x^4-x^2+x-2
=2x^4+2x^3+x-1

`a)`
`@Q(x)=x^3+2x^4-4x-4-5x^4`
`=(2x^4-5x^4)+x^3-4x-4`
`=-3x^4+x^3-4x-4`
`@P(x)-Q(x)=-2x^4+x^3+2x^2-4x-1+3x^4-x^3+4x+4`
`=x^4+2x^2+3`
______________________________________
`b)P(x)-Q(x)=0`
`=>x^4+2x^2+3=0`
`=>(x^2)^2+2x^2+1+2=0`
`=>(x^2+1)^2+2=0`
`=>(x^2+1)^2=-2` (Vô lí vì `(x^2+1)^2 >= 0` mà `-2 < 0`)
Vậy đa thức `P(x)-Q(x)` không có nghiệm

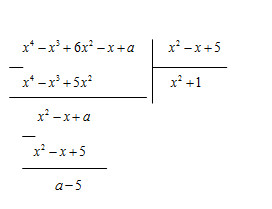
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5

Theo đề bài ta có \(M(x) = 2{x^4} - 5{x^3} + 7{x^2} + 3x\)
\(\begin{array}{l}M(x) + Q(x) = 6{x^5} - {x^4} + 3{x^2} - 2\\ \Rightarrow Q(x) = (6{x^5} - {x^4} + 3{x^2} - 2) - (2{x^4} - 5{x^3} + 7{x^2} + 3x)\\ \Rightarrow Q(x) = 6{x^5} - {x^4} + 3{x^2} - 2 - 2{x^4} + 5{x^3} - 7{x^2} - 3x\\Q(x) = 6{x^5} - 3{x^4} + 5{x^3} - 4{x^2} - 3x - 2\end{array}\)
Theo đề bài ta có :
\(\begin{array}{l}N(x) - M(x) = - 4{x^4} - 2{x^3} + 6{x^2} + 7\\ \Rightarrow N(x) = - 4{x^4} - 2{x^3} + 6{x^2} + 7 + 2{x^4} - 5{x^3} + 7{x^2} + 3x\\ \Rightarrow N(x) = - 2{x^4} - 7{x^3} + 13{x^2} + 3x + 7\end{array}\)
Chọn C
Ta có: P(x) + Q(x) = x3+ x2+ 2x-1
⇒ Q(x) = (x3 + x2 + 2x-1) - P(x)
= 2x3 + 4x2 - 8x - 3.