Giá trị của biểu thức: sin 59 0 - cos 31 0 bằng:
A.0
B.cos 28 0
C.sin 28 0
D.0,5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bạn kiểm tra lại đề, có vẻ như trong 2 cái \(sin^2\) kia phải có 1 cái là \(cos^2\) mới hợp lý

\(A = \cos {75^0}\cos {15^0} = \frac{1}{2}\left[ {\cos \left( {{{75}^0} - {{15}^0}} \right) + \cos \left( {{{75}^0} + {{15}^0}} \right)} \right] \\= \frac{1}{2}.\cos {60^0}.\cos {90^0} = 0\)
\(B = \sin \frac{{5\pi }}{{12}}\cos \frac{{7\pi }}{{12}} = \frac{1}{2}\left[ {\sin \left( {\frac{{5\pi }}{{12}} - \frac{{7\pi }}{{12}}} \right) + \sin \left( {\frac{{5\pi }}{{12}} + \frac{{7\pi }}{{12}}} \right)} \right] \\= \frac{1}{2}\sin \left( { - \frac{{2\pi }}{{12}}} \right).\sin \left( {\frac{{12\pi }}{{12}}} \right) = - \frac{1}{2}\sin \frac{\pi }{6}\sin \pi = 0\)

Vì sin(\(\alpha\) ) = cos (\(90-\alpha\)) nên \(sin^2\alpha=cos^2\left(90-\alpha\right)\)
a/ \(sin^230-sin^240-sin^250+sin^260=\left(cos^260+sin^260\right)-\left(cos^250+sin^250\right)=1-1=0\)
b/ \(cos^225-cos^235+cos^245-cos^255+cos^265=\left(sin^265+cos^265\right)-\left(sin^255+cos^255\right)+cos^245=1-1+cos^245=cos^245=\dfrac{1}{2}\)

Chọn C.
Ta có :
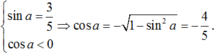
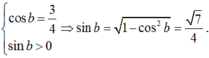
Áp dụng công thức cộng ta có:
sin(a – b) = sin a.cos b – cos a.sin b
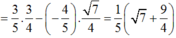

Có
A=\(\left(sin^215^o+sin^275^o\right)+\left(sin^240^o+sin^250^o\right)+\left(sin^260^o+sin^230^o\right)\)
\(=\left(sin^215^o+cos^215^o\right)+...\)
\(=1\cdot3=3\)
Câu c tương tự mà mk nghĩ đề sai dấu - trước cos^245độ
Nói chung nếu: a+b=90 độ
thì: \(sin^2a+sin^2b=1\)
b) thì áp dụng nếu a+b=90 độ:
\(tana=cotb\) và ngược lại
Mà \(tana\cdot cota=1\)
Nói chung là công thức......

Chú ý 2 điều: \(\cos45^o=\sin45^o=\frac{\sqrt{2}}{2}\) và \(\cos^2a+\sin^2a=1\)
Do đó:
a) \(A=\cos^252^o.\frac{\sqrt{2}}{2}+\sin^252^o.\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}\left(\cos^252^o+\sin^252^o\right)=\frac{\sqrt{2}}{2}.1=\frac{\sqrt{2}}{2}\)
b) \(B=\frac{\sqrt{2}}{2}.\cos^247^o+\frac{\sqrt{2}}{2}.\sin^247^o=\frac{\sqrt{2}}{2}\left(\cos^247^o+\sin^247^o\right)=\frac{\sqrt{2}}{2}.1=\frac{\sqrt{2}}{2}\)
Đáp án là A