Tìm x, biết:
a) x - 3 10 = 7 15 : 3 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
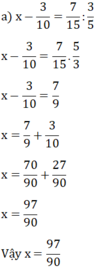
a)
\(\begin{array}{l}x + \left( { - \frac{1}{5}} \right) = \frac{{ - 4}}{{15}}\\x = \frac{{ - 4}}{{15}} + \frac{1}{5}\\x = \frac{{ - 4}}{{15}} + \frac{3}{{15}}\\x = \frac{{ - 1}}{{15}}\end{array}\)
Vậy \(x = \frac{{ - 1}}{{15}}\).
b)
\(\begin{array}{l}3,7 - x = \frac{7}{{10}}\\x = 3,7 - \frac{7}{{10}}\\x = \frac{{37}}{{10}} - \frac{7}{{10}}\\x=\frac{30}{10}\\x = 3\end{array}\)
Vậy \(x = 3\).
c)
\(\begin{array}{l}x.\frac{3}{2} = 2,4\\x.\frac{3}{2} = \frac{{12}}{5}\\x = \frac{{12}}{5}:\frac{3}{2}\\x = \frac{{12}}{5}.\frac{2}{3}\\x = \frac{8}{5}\end{array}\)
Vậy \(x = \frac{8}{5}\)
d)
\(\begin{array}{l}3,2:x = - \frac{6}{{11}}\\\frac{{16}}{5}:x = - \frac{6}{{11}}\\x = \frac{{16}}{5}:\left( { - \frac{6}{{11}}} \right)\\x = \frac{{16}}{5}.\frac{{ - 11}}{6}\\x = \frac{{ - 88}}{{15}}\end{array}\)
Vậy \(x = \frac{{ - 88}}{{15}}\).
R
19 tháng 11 2021
Bài 1:
a)-54
b)-8
Bài 2:
a)(x-14):5=415:413
⇔(x-14):5=42
⇔(x-14):5=16
⇔x-14=80
⇔x=94
b)7x-15x=15-175
⇔-8x=-160
⇔x=20
TM
1
TG
26 tháng 3 2022
a,-4/7=x/21
-12/21 = x/21
x= -12
b,(x-3)/15=1/-5
x - 3 = -1/5 * 15
x - 3 = -3
x = 0
c,.(3x+8)/-12=-5/30
=> 3x + 8 = 2
=> 3x=-6
=>x=-2
5 tháng 1 2023
a: \(\Leftrightarrow\dfrac{x}{-4}=\dfrac{21}{y}=\dfrac{z}{-80}=\dfrac{3}{4}\)
=>x=-3; y=28; z=-60
b: 5/12=x/-72
=>x=-72*5/12=-6*5=-30
c: =>x+3=-5
=>x=-8
1 tháng 11 2021
a) \(\Rightarrow\left(2x-3\right)^2=49\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow\left(x-5\right)\left(2x+7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{7}{2}\end{matrix}\right.\)
c) \(\Rightarrow x\left(x-5\right)+2\left(x-5\right)=0\Rightarrow\left(x-5\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
LN
1 tháng 11 2021
a, ⇒ (2x - 3)2 = 49
⇒ (2x - 3)2 = \(\left(\pm7\right)^2\)
⇒ \(\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=10\\2x=-4\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
b, ⇒ 2x.(x - 5) + 7.(x - 5) = 0
⇒ (x - 5).(2x + 7) = 0
⇒ \(\left[{}\begin{matrix}x-5=0\\2x+7=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=5\\2x=-7\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{7}{2}\end{matrix}\right.\)
c, ⇒ x2 - 5x + 2x - 10 = 0
⇒ (x2 - 5x) + (2x - 10) = 0
⇒ x.(x - 5) +2.(x - 5) = 0
⇒ (x - 5).(x + 2)=0
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x-5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=5\end{matrix}\right.\)
TY
2
14 tháng 2 2022
a: =>x/-3=3
hay x=-9
b: =>x/9=-1/9
hay x=-1
c: =>x+1/5=-1/3
hay x=-8/15
d: =>-7/x=-7/9
hay x=9
14 tháng 2 2022
a, \(\dfrac{x}{-3}=3\Leftrightarrow x=-9\)
b, \(\dfrac{x}{9}=-\dfrac{1}{9}\Rightarrow x=-1\)
c, \(\dfrac{x+3}{15}=-\dfrac{6}{15}\Rightarrow x=-9\)
d, \(\dfrac{42}{-54}=-\dfrac{42}{6x}\Rightarrow6x=54\Leftrightarrow x=9\)