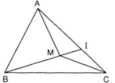
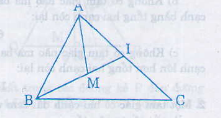
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.
a) so sánh MA với MI+IA, từ đó chứng minh MA+MB<IB+IA
b) so sánh IB với IC+IB, từ đó chứng minh IB+IA<CA+CB
c) chứng minh bất đẳng thức MA+MB<CA+CB