Cho a=5 và b-c=20. Biết A = b(a-c)-c(a-b).
Giá trị của A là ...........
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
2
N
2 tháng 2 2018
A2 = ba -bc -ca +bc = ba - ca = a(b-c) Với a = -20 , b-c = -5 thì A2 = (-20).(-5)= 100 suy ra A = 10 hoặc -10
2 tháng 2 2018
A2 = b(a - c) - c(a - b)
= ab - bc - ac + bc
= ab - ac
= a.(b - c)
Thay a = -20, b - c = -5
=> A2 = -20.(-5)
= 100
=> A = 10
VT
10 tháng 12 2019
Ta có vật AB và ảnh A1B1 cùng thật và ngược chiều, nên k1 < 0; AB → A1B1
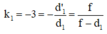
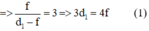
Tương ứng với vị trí sau của vật AB thật và ảnh A2B2 ảo cùng chiều nên k2 > 0.
Vật di chuyển lại gần nên d2 = d1 - 12
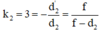
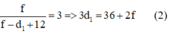
Từ (1) và (2) ta có: 4f = 36 + 2f → f = 18cm
Đáp án: B
NC
24 tháng 8 2020
Bài làm:
Ta có: \(A^2=b\left(a-c\right)-c\left(a-b\right)\)
\(A^2=ab-bc-ac+bc\)
\(A^2=ab-ac=a\left(b-c\right)\)
\(A^2=\left(-5\right).\left(-20\right)=100\)
\(\Rightarrow\orbr{\begin{cases}A=10\\A=-10\end{cases}}\)
18 tháng 12 2016
Ta có:\(\frac{a}{b+c+d}=\frac{b}{c+d+a}=\frac{c}{a+b+d}=\frac{d}{a+b+c}\)
\(\Rightarrow\frac{b+c+d}{a}=\frac{c+d+a}{b}=\frac{a+b+d}{c}=\frac{a+b+c}{d}\)
\(\Rightarrow\frac{b+c+d}{a}+1=\frac{c+d+a}{b}+1=\frac{a+b+d}{c}+1=\frac{a+b+c}{d}+1\)
\(\Rightarrow\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)=\(\frac{a+b+c+d+a+b+c+d+a+b+c+d+a+b+c+d}{a+b+c+d}=4\)(T/C)
Xét a+b+c+d=0
\(\Rightarrow a+c=-\left(b+d\right),a+b=-\left(c+d\right),b+c=-\left(a+d\right)\)
\(\Rightarrow M=-1+-1+-1+-1=-4\)
Xét \(a+b+c+d\ne0\Rightarrow a=b=c=d\)
\(\Rightarrow M=1+1+1+1=4\)
Vậy M=-4 hoặc M=4
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 8 2023
a, a x 6 = 3 x 6 = 18
b, a + b = 4 + 2 = 6
c, b + a = 2 + 4 = 6
d, a - b = 8 - 5 = 3
e, m x n = 5 x 9 = 45
A = b(a - c) - c(a - b)
= ab - bc - ac + bc
= ab - ac
= a(b - c) = 5 . 20 = 100
Vậy A = 100