cho 3x-4y=0;tìm min của M=x^2+y^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường thẳng song song d nên nhận (3;-4) là 1 vtpt
Phương trình:
\(3\left(x-2\right)-4\left(y-1\right)=0\Leftrightarrow3x-4y-2=0\)

Gọi M là giao điểm của \(d_1\) và \(d_2\Rightarrow\) toạ độ M là nghiệm của hệ:
\(\left\{{}\begin{matrix}3x-2y+5=0\\2x+4y-7=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{3}{8};\frac{31}{16}\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x+\frac{3}{8}\right)+4\left(y-\frac{31}{16}\right)=0\Leftrightarrow24x+32y-53=0\)

Ta có: \(\frac{x+2y}{3x+4y}=\frac{2}{5}\)
=> (x + 2y).5 = 2.(3x + 4y)
=> 5x + 10y = 6x + 8y
=> 10y - 8y = 6x - 5x
=> 2y = x
=> \(\frac{2y}{x}=1\)
Vậy \(\frac{2y}{x}=1\)

Gọi d là \(3x-4y-18=0\) và d' là \(3x-4y+1=0\)
Chọn \(A\left(6;0\right)\) là điểm thuộc d
\(\Rightarrow d\left(d;d'\right)=d\left(A;d'\right)=\frac{\left|3.6-4.0+1\right|}{\sqrt{3^2+\left(-4\right)^2}}=\frac{19}{5}\)

Đáp án B
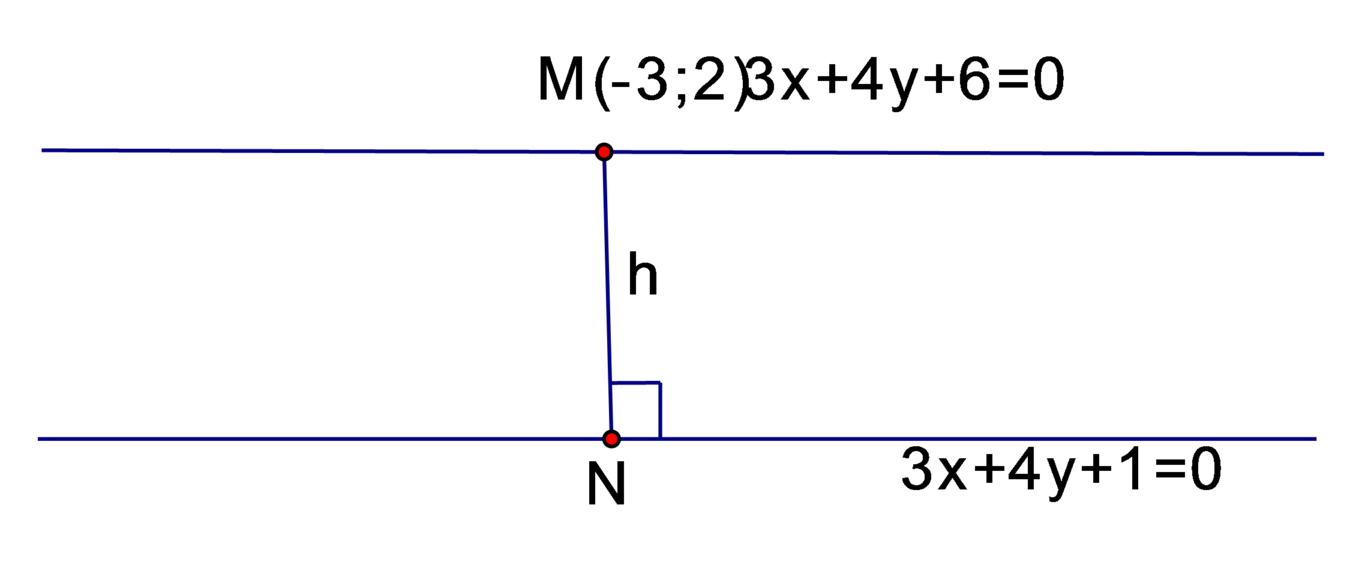
Độ dài véc tơ v → bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó: v → = M N →
Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:
M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3
⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5
⇒ M N → = − 3 5 ; − 4 5

Do tâm I của đường tròn thuộc d nên tọa độ I có dạng \(I\left(6a+10;a\right)\)
Đường tròn tiếp xúc d1 và d2
\(\Leftrightarrow d\left(I;d_1\right)=d\left(I;d_2\right)\)
\(\Leftrightarrow\frac{\left|3\left(6a+10\right)+4a+5\right|}{\sqrt{3^2+4^2}}=\frac{\left|3\left(6a+10\right)-4a-5\right|}{\sqrt{3^2+\left(-4\right)^2}}\)
\(\Leftrightarrow\left|22a+35\right|=\left|14a+25\right|\)
\(\Rightarrow\left[{}\begin{matrix}22a+35=14a+25\\22a+35=-14a-25\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}a=-\frac{5}{4}\\a=-\frac{5}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(\frac{5}{2};-\frac{5}{4}\right)\\I\left(0;-\frac{5}{3}\right)\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn:
\(\left[{}\begin{matrix}\left(x-\frac{5}{2}\right)^2+\left(y+\frac{5}{4}\right)^2=\frac{9}{4}\\x^2+\left(y+\frac{5}{3}\right)^2=\frac{1}{9}\end{matrix}\right.\)

Hai đường thẳng song song khi m 3 = 2 − 4 ≠ − 3 2 n ê n m = − 3 2
Chọn đáp án C.


ta có:
3x-4y=0
=>3x=4y=>3/4=y/x( nếu chưa tối giản thì bạn giút gọn đi)
=>y=3;x=4
thay vào bài ta có:M=4^2+3^2=16+9=25
vậy giá trị nhỏ nhất của M là 25
k nhé @@@