(x-5)^2=(-x+5)^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(2+2+2+2+2=2\times5=10\)
\(2\times5=10\)
\(5+5=2\times5=10\)
\(5\times2=10\)
b) \(3\times5=3+3+3+3+3=15\)
\(5\times3=5+5+5=15\)
\(3\times5=5+5+5=15\)
\(5\times3=3+3+3+3+3=15\)
a) 2 + 2 + 2 + 2 + 2 = 10
2 x 5 = 10
5 + 5 = 10
5 x 2 = 10
b) 3 x 5 = 3 + 3 + 3 + 3 + 3 = 15
5 x 3 = 5 + 5 + 5 = 15
3 x 5 = 15
5 x 3 = 15

a: =>x-2/5=3/4:1/3=3/4*3=9/4
=>x=9/4+2/5=45/20+8/20=53/20
b: =>x-2/3=7/3:4/5=7/3*5/4=35/12
=>x=35/12+2/3=43/12
c: 1/3(x-2/5)=4/5
=>x-2/5=4/5*3=12/5
=>x=12/5+2/5=14/5
d: =>2/3x-1/3-1/4x+1/10=7/3
=>5/12x-7/30=7/3
=>5/12x=7/3+7/30=77/30
=>x=77/30:5/12=154/25
e: \(\Leftrightarrow x\cdot\dfrac{3}{7}-\dfrac{2}{7}+\dfrac{1}{2}-\dfrac{5}{4}x+\dfrac{5}{2}=0\)
=>\(x\cdot\dfrac{-23}{28}=\dfrac{2}{7}-3=\dfrac{-19}{7}\)
=>x=19/7:23/28=76/23
f: =>1/2x-3/2+1/3x-4/3+1/4x-5/4=1/5
=>13/12x=1/5+3/2+4/3+5/4=257/60
=>x=257/65
i: =>x^2-2/5x-x^2-2x+11/4=4/3
=>-12/5x=4/3-11/4=-17/12
=>x=17/12:12/5=85/144

2:
a: =>x^2+3x-4x-12-(x^2-5x+x-5)=8
=>x^2-x-12-x^2+4x+5=8
=>3x-7=8
=>3x=15
=>x=5
b: =>3x^2+3x-2x-2-3x^2-21x=13
=>-20x=15
=>x=-3/4
c: =>x^2-25-x^2-2x=9
=>-2x=25+9=34
=>x=-17
d: =>x^3-1-x^3+3x=1
=>3x-1=1
=>3x=2
=>x=2/3

Bài 1:
a) \(-5\left(x^2-3x+1\right)+x\left(1+5x\right)=x-2\)
\(\Rightarrow-5x^2+15x-5+x+5x^2=x-2\)
\(\Rightarrow16x-5=x-2\)
\(\Rightarrow16x-x=5-2\)
\(\Rightarrow15x=3\)
\(\Rightarrow x=\dfrac{15}{3}=5\)
b) \(12x^2-4x\left(3x+5\right)=10x-17\)
\(\Rightarrow12x^2-12x^2-20x=10x-17\)
\(\Rightarrow-20x=10x-17\)
\(\Rightarrow-20x-10x=-17\)
\(\Rightarrow-30x=-17\)
\(\Rightarrow x=\dfrac{-30}{-17}=\dfrac{30}{17}\)
c) \(-4x\left(x-5\right)+7x\left(x-4\right)-3x^2=12\)
\(\Rightarrow-4x^2+20x+7x^2-28x-3x^2=12\)
\(\Rightarrow-8x=12\)
\(\Rightarrow x=\dfrac{12}{-8}=-\dfrac{4}{3}\)
Bài 2:
a) \(\left(x+5\right)\left(x-7\right)-7x\left(x-3\right)\)
\(=x^2-7x+5x-35-7x^2+21x\)
\(=-6x^2+19x-35\)
b) \(x\left(x^2-x-2\right)-\left(x-5\right)\left(x+1\right)\)
\(=x^3-x^2-2x-x^2+x-5x-5\)
\(=x^3-2x^2-6x-5\)
c) \(\left(x-5\right)\left(x-7\right)-\left(x+4\right)\left(x-3\right)\)
\(=x^2-7x-5x+35-x^2-3x+4x-12\)
\(=11x+23\)
d) \(\left(x-1\right)\left(x-2\right)-\left(x+5\right)\left(x+2\right)\)
\(=x^2-2x-x+2-x^2+2x+5x+10\)
\(=4x+12\)

1) \(2^3\times x-5^2\times x=2\times\left(5^2+2^2\right)-33\)
\(x\times\left(2^3-5^2\right)=2\times\left(25+4\right)-33\)
\(x\times\left(8-25\right)=2\times29-33\)
\(x\times-17=25\)
\(x=-\dfrac{25}{17}\)
2) \(15\div\left(x+2\right)=\left(3^3+3\right)\div1\)
\(15\div\left(x+2\right)=\left(27+3\right)\div1\)
\(15\div\left(x+2\right)=30\div1\)
\(15\div\left(x+2\right)=30\)
\(x+2=\dfrac{1}{2}\)
\(x=-\dfrac{3}{2}\)
3) \(20\div\left(x+1\right)=\left(5^2+1\right)\div13\)
\(20\div\left(x+1\right)=\left(25+1\right)\div13\)
\(20\div\left(x+1\right)=26\div13\)
\(20\div\left(x+1\right)=2\)
\(x+1=20\div2\)
\(x+1=10\)
\(x=9\)
4) \(320\div\left(x-1\right)=\left(5^3-5^2\right)\div4+15\)
\(320\div\left(x-1\right)=\left(125-25\right)\div4+15\)
\(320\div\left(x-1\right)=100\div4+15\)
\(320\div\left(x-1\right)=25+15\)
\(320\div\left(x-1\right)=40\)
\(x-1=8\)
\(x=9\)
5) \(240\div\left(x-5\right)=2^2\times5^2-20\)
\(240\div\left(x-5\right)=4\times25-20\)
\(240\div\left(x-5\right)=100-20\)
\(240\div\left(x-5\right)=80\)
\(x-5=30\)
\(x=35\)
6) \(70\div\left(x-3\right)=\left(3^4-1\right)\div4-10\)
\(70\div\left(x-3\right)=\left(81-1\right)\div4-10\)
\(70\div\left(x-3\right)=80\div4-10\)
\(70\div\left(x-3\right)=20-10\)
\(70\div\left(x-3\right)=10\)
\(x-3=7\)
\(x=10\)

\(\Leftrightarrow\left(x-5\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\\ \Rightarrow C\)

1.
$(x-2)(x-5)=(x-3)(x-4)$
$\Leftrightarrow x^2-7x+10=x^2-7x+12$
$\Leftrightarrow 10=12$ (vô lý)
Vậy pt vô nghiệm.
2.
$(x-7)(x+7)+x^2-2=2(x^2+5)$
$\Leftrightarrow x^2-49+x^2-2=2x^2+10$
$\Leftrightarrow 2x^2-51=2x^2+10$
$\Leftrightarrow -51=10$ (vô lý)
Vậy pt vô nghiệm.
3.
$(x-1)^2+(x+3)^2=2(x-2)(x+2)$
$\Leftrightarrow (x^2-2x+1)+(x^2+6x+9)=2(x^2-4)$
$\Leftrightarrow 2x^2+4x+10=2x^2-8$
$\Leftrightarrow 4x+10=-8$
$\Leftrightarrow 4x=-18$
$\Leftrightarrow x=-4,5$
4.
$(x+1)^2=(x+3)(x-2)$
$\Leftrightarrow x^2+2x+1=x^2+x-6$
$\Leftrightarrow x=-7$

1; 5.22 + (\(x\) + 3) = 52
5.4 + (\(x\) + 3) = 25
20 + (\(x\) + 3) = 25
\(x\) + 3 = 25 - 20
\(x+3\) = 5
\(x\) = 5 - 3
\(x\) = 2
Vậy \(x=2\)
2; 23 + (\(x\) - 32) = 53 - 43
8 + (\(x\) - 9) = 125 - 64
8 + (\(x\) - 9) = 61
\(x\) - 9 = 61 - 8
\(x\) - 9 = 53
\(x\) = 53 + 9
\(x\) = 62
Vậy \(x\) = 62

1: Ta có: \(x^2-2x+5-\left(x-7\right)\left(x+2\right)\)
\(=x^2-2x+5-x^2-2x+7x-14\)
\(=3x-9\)
2: Ta có: \(-5x\left(x-5\right)+\left(x-3\right)\left(x^2-7\right)\)
\(=-5x^2+25x+x^3-7x-3x^2+21\)
\(=x^3-8x^2+18x+21\)
3: Ta có: \(x\left(x^2-x-2\right)-\left(x+5\right)\left(x-1\right)\)
\(=x^3-x^2-2x-x^2-4x+5\)
\(=x^3-2x^2-6x+5\)
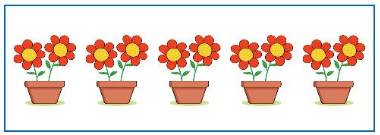

 =
= 
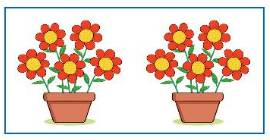

 =
= 
 3 x 5 =
3 x 5 = 
 5 x 3 =
5 x 3 = 
\(\left(x-5\right)^2=\left(-x+5\right)^2\)
\(\Leftrightarrow\left(x-5\right)^2=\left[-\left(x-5\right)\right]^2\)
\(\Leftrightarrow\left(x-5\right)^2=\left(x-5\right)^2\)
\(\Leftrightarrow\left(x-5\right)^2-\left(x-5\right)^2=0\)
\(\Leftrightarrow0x=0\)( luôn đúng )
Vậy nghiệm của phương trình là \(x\inℝ\)