Hình thoi ABCD có góc A = 60°. Trên cạnh AD lấy điểm M, trên cạnh CD lấy điểm N sao cho AM = DN.
a)Tam giác BMN là tam giác gì? Vì sao?
b)tìm vị trí của M trên AD để tam giác BMN có chu vi nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

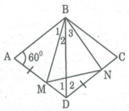
Nối BD, ta có AB = AD (gt)
Suy ra ∆ ABD cân tại A
Mà ∠ A = 60 0 ⇒ ∆ ABD đều
⇒ ∠ (ABD) = ∠ D 1 = 60 0 và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều ⇒ ∠ D 2 = 60 0
Xét ∆ BAM và ∆ BDN,ta có:
AB = BD ( chứng minh trên)
∠ A = ∠ D 2 = 60 0
AM = DN (giả thiết)
Do đó ∆ BAM = ∆ BDN ( c.g.c) ⇒ ∠ B 1 = ∠ B 3 và BM = BN
Suy ra ΔBMN cân tại B.
Mà ∠ B 2 + ∠ B 1 = ∠ (ABD) = 60 0
Suy ra: ∠ B 2 + ∠ B 3 = ∠ B 2 + ∠ B 1 = 60° hay ∠ (MBN) = 60 0
Vậy ∆ BMN đều

Xét ΔABD có AB=AD và góc A=60 độ
=>ΔABD đều
=>góc ABD=góc ADB=60 độ và AB=AD=BD
Xét ΔBCD có CB=CD và góc C=60 độ
nên ΔBCD đều
=>BD=CB=CD và góc CBD=góc CDB=60 độ
Xét ΔBAM và ΔBDN có
BA=BD
góc BAM=góc BDN
AM=DN
=>ΔBAM=ΔBDN
=>BM=BN và góc ABM=góc DBN
=>góc DBN+góc DBM=60 độ
=>góc MBN=60 độ
=>ΔMBN đều
https://tailieumoi.vn/cau-hoi/hinh-thoi-abcd-co-goc-a-60-do-tren-canh-ad-lay-diem-m-tren-canh-137282.html
Nhắc lần thứ nhất, không copy câu trả lời từ nguồn khác.

a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ

Đặt AM=x; AN=y
MN^2=AM^2+AN^2
=>\(MN=\sqrt{x^2+y^2}\)
\(P_{AMN}=AM+AN+MN=x+y+\sqrt{x^2+y^2}=2a\)
và x+y>=2*căn xy; \(\sqrt{x^2+y^2}>=\sqrt{2xy}\)
=>\(2a=x+y+\sqrt{x^2+y^2}>=2\sqrt{xy}+\sqrt{2xy}\)
=>\(2a>=\sqrt{xy}\left(2+\sqrt{2}\right)\)
=>\(\sqrt{xy}< =\dfrac{2a}{2+\sqrt{2}}\)
=>\(S_{AMN}=\dfrac{1}{2}xy< =\dfrac{1}{2}\cdot\left(\dfrac{2a}{2+\sqrt{2}}\right)^2=\left(3-2\sqrt{2}\right)a^2\)
Dấu = xảy ra khi \(x=y=\left(2-\sqrt{2}\right)a\)
giúp mình nha người đầu tiên