Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tứ giác adch có góc cha=90 độ và hai đường chéo cắt nhau tại trung điểm mỗi đoạn( trở thành hbh) => adch là hcn
b, do adch là hcn nên ad//ch=>ad//he và ad=ch => ad= he.
=> adhe là hbh

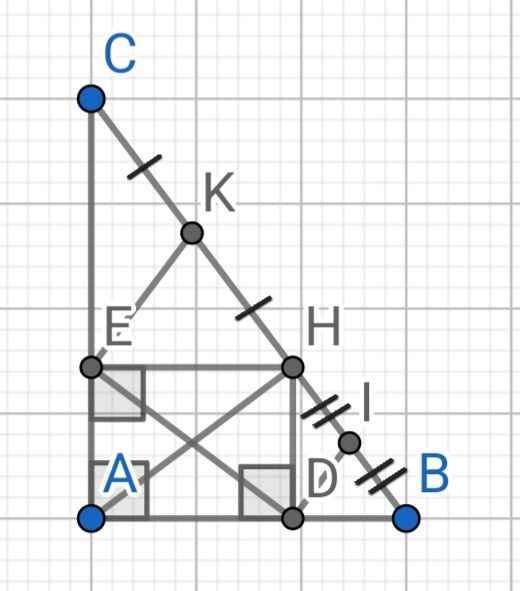 a) Tứ giác ADHE có:
a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE

b: Xét tứ giác AMHI có
AM//HI
HM//AI
Do đó: AMHI là hình bình hành
mà \(\widehat{MAI}=90^0\)
nên AMHI là hình chữ nhật
Suy ra: AH=MI

a: Xét tứ giác AHDE có
I là trung điểm của AD
I là trung điểm của HE
Do đó: AHDE là hình bình hành
mà AD⊥HE
nên AHDE là hình thoi