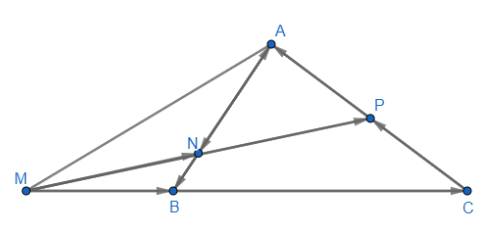
Cho tam giác ABC , điểm M xác định bởi\(\overrightarrow{BM}=\overrightarrow{BC}-2\overrightarrow{AB}\) , điểm N thỏa mãn \(\overrightarrow{CN}=x\overrightarrow{AC}-\overrightarrow{BC}\)
Tìm x để đường thẳng MN đi qua trung điểm I của BC.
A. x=2/5
B x =-2/5
C x=2/3
D x= -2/3



\(\overrightarrow{BM}=\overrightarrow{BC}-2\overrightarrow{AB}\Leftrightarrow\overrightarrow{BI}+\overrightarrow{IM}=\overrightarrow{BC}-2\left(\overrightarrow{AC}+\overrightarrow{CB}\right)\)
\(\Leftrightarrow\frac{1}{2}\overrightarrow{BC}+\overrightarrow{IM}=\overrightarrow{BC}-2\overrightarrow{AC}+2\overrightarrow{BC}\Rightarrow\overrightarrow{IM}=\frac{5}{2}\overrightarrow{BC}-2\overrightarrow{AC}\)
\(\overrightarrow{CI}+\overrightarrow{IN}=x\overrightarrow{AC}-\overrightarrow{BC}\Rightarrow-\frac{1}{2}\overrightarrow{BC}+\overrightarrow{IN}=x\overrightarrow{AC}-\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{IN}=-\frac{1}{2}\overrightarrow{BC}+x\overrightarrow{AC}=-\frac{1}{5}\left(\frac{5}{2}\overrightarrow{BC}-5x.\overrightarrow{AC}\right)\)
Để MN qua I hay I;M;N thẳng hàng \(\Leftrightarrow5x=2\Rightarrow x=\frac{2}{5}\)