Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau.
Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \)
b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \)
Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)

a)
- \(\overrightarrow{BI}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\) (t/c trung điểm)
\(=\frac{1}{2}\left(\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}\right)\)
\(=\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\)
- \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}+\frac{1}{3}\left(\overrightarrow{BC}-\overrightarrow{BA}\right)\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}-\frac{1}{3}\overrightarrow{BA}\)
\(=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}\)
b) Ta có: \(\overrightarrow{BK}=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}=\frac{4}{3}\left(\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\right)=\frac{4}{3}\overrightarrow{BI}\)
=> B,K,I thẳng hàng
c) \(27\overrightarrow{MA}-8\overrightarrow{MB}=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\left(\overrightarrow{MC}+\overrightarrow{CA}\right)-8\left(\overrightarrow{MC}+\overrightarrow{CB}\right)=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{MC}-8\overrightarrow{CB}-2015\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow-1996\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{CB}=\overrightarrow{0}\)
\(\Leftrightarrow1996\overrightarrow{CM}=8\overrightarrow{CB}-27\overrightarrow{CA}\)
\(\Leftrightarrow\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)
Vậy: Dựng điểm M sao cho \(\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)

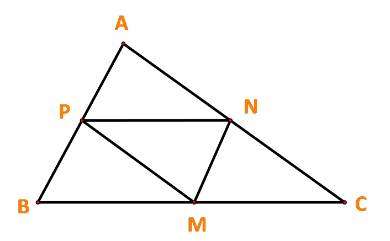
a) Ta có: \(\overrightarrow {BC} ,\overrightarrow {PN} \) là hai vecto cùng hướng và \(\frac{1}{2}\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {PN} } \right|\)
\( \Rightarrow \frac{1}{2}\overrightarrow {BC} = \overrightarrow {PN} \)\( \Rightarrow \overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AP} + \overrightarrow {PN} = \overrightarrow {AN} \)
b) Ta có: \(\overrightarrow {MP} ,\overrightarrow {CA} \) là hai vecto cùng hướng và \(2\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {CA} } \right|\)
\( \Rightarrow 2\overrightarrow {MP} = \overrightarrow {CA} \)\( \Rightarrow \overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA} \)

Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
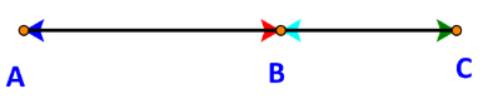
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);
a) Ta có:
+) \(\overrightarrow {MB} = \dfrac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\dfrac{{BC}}{{MB}} = 2\)
\( \Rightarrow M\) nằm ngoài đoạn thẳng BC sao cho \(MB = \dfrac{1}{2}BC\)
+) \({\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \dfrac{1}{4}\overrightarrow {AB} }\)
\( \Rightarrow N\) thuộc đoạn thẳng AB và \(NB=\dfrac{{1}}{{4}} AB\)
+) \(\overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0 \)
\( \Rightarrow P\) là trung điểm của CA
b) \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} \)
\(\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}\)
c) Ta có:
\(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ;\) \(\overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \)
\( \Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN} \)
Vậy \(M,N,P\) thẳng hàng