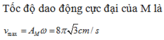Tốc độ của 1 chiếc cannô vàđộ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức v=5$\sqrt{l}$ . Trong đó,l là độ dài đường nước sau đuôi cannô( mét), v là vận tốc canno (m/giây).Hỏi...

TN

Thị nga Hoàng

11 tháng 10 2020 - olm

Tốc độ của 1 chiếc cannô vàđộ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức v=5$\sqrt{l}$ . Trong đó,l là độ dài đường nước sau đuôi cannô( mét), v là vận tốc canno (m/giây).Hỏi cannô đi từ Nam Căn về huyện đất Mũi (Cà Mau) để lại đường sóng nươcsau đuôi dài 7+4$\sqrt{3}$ m. Thì có vận tốc là...

Đọc tiếp

#Toán lớp 9

0

B

Buddy

17 tháng 8 2023

Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức $h = 19,6t - 4,9{t^2}.$ Tìm vận tốc của vật khi nó chạm đất.

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

Với ${x_0}$ bất kì, ta có:

$f'\left( {{t_0}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{19,6t - 4,9{t^2} - 19,6{t_0} + 4,9t_0^2}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \frac{{ - 4,9\left( {{t^2} - t_0^2} \right) + 19,6\left( {t - {t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \frac{{\left( {t - {t_0}} \right)\left( { - 4,9t - 4,9{t_0} + 19,6} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( { - 4,9t - 4,9{t_0} + 19,6} \right) = - 9,8{t_0} + 19,6$

Vậy hàm số $h = 19,6t - 4,9{t^2}$ có đạo hàm là hàm số $h' = - 9,8{t_0} + 19,6$

Độ cao của vật khi nó chạm đất thỏa mãn $19,6t - 4,9{t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 4\end{array} \right.$

Khi t = 4, vận tốc của vật khi nó chạm đất là $ - 9,8.4 + 19,6 = - 19,6$ (m/s)

Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.

Đúng(0)

HD

Hoàng Đức Long

30 tháng 4 2018

Sóng dừng trên sợ dây đàn hồi OB có chiều dài L = 60cm được mô tả như hình bên. Điểm O trùng với gốc tọa độ của trục tung. Sóng tới điểm B có biên độ a = 2 cm. Thời điểm ban đầu hình ảnh sóng là đường (1), sau thời gian ∆ t và 5 ∆ t thì hình ảnh sóng lần lượt là đường (2) và đường (3). Tốc độ truyền sóng là v= 1,2 m/s. Tốc độ dao động cực đại của...

Đọc tiếp

#Vật lý lớp 12

1

VT

Vũ Thành Nam

30 tháng 4 2018

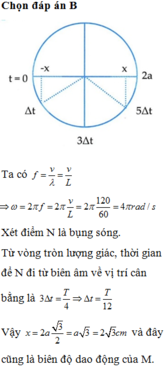
Đáp án B

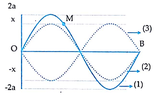
Ta có

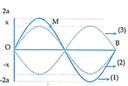
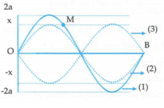
Xét điểm N là bụng sóng.

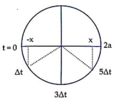
Từ vòng tròn lượng giác thời gian để N đi từ biên âm về vị trí cân bằng là

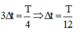
Vậy 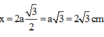và đây cũng là biên ođọ dao động của M.

Tốc độ dao động cực đại của M là

.

Đúng(0)

HD

Hoàng Đức Long

7 tháng 4 2018

Sóng dừng trên sợi dây đàn hồi OB có chiều dài L = 60 cm được mô tả như hình bên. Điểm O trùng với gốc tọa độ của trục tung. Sóng tới điểm B có biên độ a = 2cm. Thời điểm ban đầu hình ảnh sóng là đường (1), sau thời gian ∆ t và 5 ∆ t thì hình ảnh sóng lần lượt là đường (2) và đường (3). Tốc độ truyền sóng là v = 1,2 m/s. Tốc độ dao động cực đại của...

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

7 tháng 4 2018

Đúng(0)

B

Buddy

20 tháng 8 2023

Một viên soi rơi từ độ cao 44,1 m thì quãng đường rơi được biểu diễn bởi công thức $s\left( t \right) = 4,9{t^2}$, trong đó $t$ là thời gian tính bằng giây và $s$ tính bằng mét. Tinh:

a) Vận tốc rơi của viên sỏi lúc $t = 2$;

b) Vận tốc của viên sỏi khi chạm đất.

#Toán lớp 11

2

H

HaNa

20 tháng 8 2023

a)

Vận tốc rơi của viên sỏi lúc `t=2`:

$v(2) = 9,8 \cdot 2 = 19.6 , \text{m/s}$

b)

Khi viên sỏi chạm đất, quãng đường rơi sẽ bằng độ cao ban đầu:

$s(t) = 4.9t^2 = 44.1$

Giải phương trình trên, ta có:

$t^2 = \frac{44.1}{4.9}$
$t \approx 3,0 \text{giây}$

$v(3.0) = 9,8 \cdot 3,0 = 29,4 \text{m/s}$

Vậy vận tốc của viên sỏi khi chạm đất là $29,4 \text{m/s}$.

Đúng(1)

NL

Nguyễn Lê Phước Thịnh

20 tháng 8 2023

a: v(t)=s'(t)=4,9*2t=9,8t

Khi t=2 thì v(2)=9,8*2=19,6(m/s)

b: Quãng đường đi được là 44,1m

=>4,9t^2=44,1

=>t=3

Khi t=3 thì v(3)=9,8*3=29,4(m/s)

Đúng(1)

HD

Hoàng Đức Long

26 tháng 7 2019

Sóng dừng trên sợ dây đàn hồi OB có chiều dài L = 60 c m được mô tả như hình bên. Điểm O trùng với gốc tọa độ của trục tung. Sóng tới điểm B có biên độ a = 2 c m . Thời điểm ban đầu hình ảnh sóng là đường (1), sau thời gian Δ t và 5 Δ t thì hình ảnh sóng lần lượt là đường (2) và đường (3). Tốc độ...

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

26 tháng 7 2019

Đáp án B

Ta có f = v λ = v L ⇒ ω = 2 π f = 2 π v L = 2 π 120 60 = 4 π r a d / s

Xét điểm N là bụng sóng

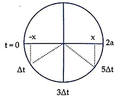
Từ vòng tròn lượng giác thời gian để N đi từ biên âm về vị trí cân bằng là 3 Δ t = T 4 ⇒ Δ t = T 12

Vậy x = 2 a 3 2 = a 3 = 2 3 c m và đây cũng là biên độ dao động của M

Tốc độ dao động cực đại của M là v max = A M ω = 8 π 3 c m / s

Đúng(0)

PT

Pham Trong Bach

31 tháng 1 2017

Đến mùa sinh sản, một con cá hồi bơi ngược dòng để vượt một quãng đường 240km. Vận tốc dòng nước là 3km/h. Nếu vận tốc bơi của cá khi nước yên lặng là v(km/h) thì năng lượng tiêu hao của con cá trong t giờ được cho bởi công thức E(v)=cv3 t, trong đó c là hằng số, E được tính bằng jun. Tìm vận tốc của con cá khi nước đứng yên để năng lượng tiêu hao là ít nhất. A. 5km/h B. 6km/h C....

Đọc tiếp

#Toán lớp 12

2

CM

Cao Minh Tâm

31 tháng 1 2017

Đúng(0)

NT

Nguyễn Thảo Ngân

16 tháng 4 2022

Đáp án D

chúc bạn họk tốt! 0ω0

Đúng(0)

HH

Hiền Hòa

22 tháng 10 2021

Vận tốc rơi tự do của một vật được tính bởi công thức: trong đó, v là vận tốc tính theo m/s, h là độ cao của vật lúc bắt đầu rơi tính bằng mét (m) và g = 9,8 m/s2 .Một vận động viên nhảy dù khi trình diễn việc rơi tự do đạt vận tốc 140 m/s. Hỏi độ cao của vận động viên đó lúc bắt đầu thực hiện động tác nhảy là bao nhiêu m ?...

Đọc tiếp

#Toán lớp 9

0

HH

hân hoàng

15 tháng 3 2023 - olm

Quãng đường chuyển động của một vật rơi tự do được biểu diễn gần đúng bởi công thức S=5t mũ 2 trong đó t là thời gian tính bằng giây , S tính bằng mét .Vận tốc của vật chuyển động rơi tự do đc cho bởi công thức V = 9,8t với t là thời gian tính bằng giây từ lúc vật bắt đầu rơi.Một vận động viên nhảy dù dự định nhảy rơi tự do từ độ cao 3970m .Vận động tính bung dù khi cách mặt đất 845m....

Đọc tiếp

#Toán lớp 7

1

ND

Nguyễn Đắc Linh

15 tháng 3 2023

Để giải bài toán này, ta sử dụng hai công thức sau:

Quãng đường chuyển động của vật rơi tự do: S = 5t²
Vận tốc của vật rơi tự do: V = 9,8t
Để tìm thời điểm vận động viên phải bật dù, ta cần tính thời gian mà vận động viên rơi từ độ cao 3970m đến cách mặt đất 845m:

Đầu tiên, ta tính quãng đường rơi của vận động viên: 3970 m - 845 m = 3125 m

Sau đó, ta sử dụng công thức quãng đường chuyển động của vật rơi tự do để tính thời gian rơi của vận động viên từ độ cao 3125m: S = 5t² 3125 = 5t² t² = 625 t = 25 giây

Vậy sau 25 giây từ lúc bắt đầu nhảy, vận động viên phải bật dù.

Để tính vận tốc rơi của vận động viên tại thời điểm cách mặt đất 845m, ta sử dụng công thức vận tốc của vật rơi tự do:

V = 9,8t

Ta thấy được rằng tại thời điểm cách mặt đất 845m, thời gian rơi của vận động viên là: S = 5t² 845 = 5t² t² = 169 t = 13 giây

Vậy sau 13 giây từ lúc bắt đầu nhảy, vận động viên cách mặt đất 845m và vận tốc rơi của vận động viên là: V = 9,8t = 9,8 x 13 = 127,4 (m/s)

Vậy sau 13 giây từ lúc bắt đầu nhảy, vận tốc rơi của vận động viên là 127,4 (m/s).

Đúng(2)

HH

hân hoàng

16 tháng 3 2023

Quãng đường chuyển động của một vật rơi tự do được biểu diễn gần đúng bởi công thức S=5t mũ 2 trong đó t là thời gian tính bằng giây , S tính bằng mét .Vận tốc của vật chuyển động rơi tự do đc cho bởi công thức V = 9,8t với t là thời gian tính bằng giây từ lúc vật bắt đầu rơi.Một vận động viên nhảy dù dự định nhảy rơi tự do từ độ cao 3970m .Vận động tính bung dù khi cách mặt đất 845m....

Đọc tiếp

#Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP