Giải phương trình:
2tan2x-2√3tanx-3=0
√3cot2x-(1+√3)cotx+1=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
US
5
Những câu hỏi liên quan
CM
1 tháng 3 2017
Điều kiện: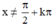 
2tan2x + 3tanx + 1 = 0 (Phương trình bậc 2 với ẩn tan x).
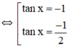
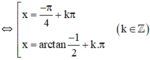(Thỏa mãn điều kiện)
Vậy phương trình có tập nghiệm {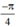
+ kπ; arctan
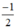+ kπ} (k ∈ Z)
PT
3
K
25 tháng 5 2021
ssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss
Y
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
ĐKXĐ: \(sin2x\ne0\Rightarrow x\ne\dfrac{k\pi}{2}\)
\(3tanx+\dfrac{\sqrt{3}}{tanx}-3-\sqrt{3}=0\)
\(\Rightarrow3tan^2x-\left(3+\sqrt{3}\right)tanx+\sqrt{3}=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
CM
24 tháng 7 2017
Đáp án A
Phương trình tương đương tan x = - 3 ⇔ x = - π 3 + k π
CM
26 tháng 9 2019
Điều kiện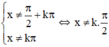 
tanx – 2.cotx + 1 = 0
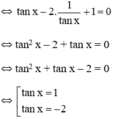
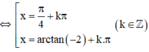(Thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
{
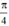+ kπ; arctan(-2) + kπ} (k ∈ Z)
\(2tan^2x-2\sqrt{3}tanx-3=0\)
\(\orbr{\begin{cases}tanx=\frac{3+\sqrt{3}}{2}\\tanx=\frac{-3+\sqrt{3}}{2}\end{cases}}\)
\(\orbr{\begin{cases}tanx=tana\\tanx=tanb\end{cases}}\) Đặt \(tana=\frac{3+\sqrt{3}}{2};tanb=\frac{-3+\sqrt{3}}{2}\)
\(\orbr{\begin{cases}x=a+k\pi\\x=b+k\pi\end{cases};k\in Z}\)
\(\sqrt{3}cot^2x-\left(1+\sqrt{3}\right)cotx+1=0\)
\(\orbr{\begin{cases}cotx=1\\cotx=\frac{\sqrt{3}}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tanx=1=tan\frac{\pi}{4}\\tanx=\sqrt{3}=tan\frac{\pi}{3}\end{cases}}\)
\(\orbr{\begin{cases}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{3}+k\pi\end{cases};k\in Z}\)
bang lon