2 đường thẳng MN và PQ cắt nhau tại O. biết \(\widehat{MOP}\)- \(\widehat{MOQ}\)= \(40^o\)
tính \(\widehat{MOP}\), \(\widehat{PON}\), \(\widehat{NOQ}\), \(\widehat{QOM}\)
nó là bài toán tổng hiệu nhưng mình quên mất cách làm rùi huhu :((((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: góc MOP+góc NOQ=160 độ
Vì góc MOP=góc NOQ(hai góc đối đỉnh)
nên góc MOP=góc NOQ=160/2=80 độ

160 độ - NOQ = ?
Mình chỉ biết thế thôi !
Bởi vì năm nay mình mới lên lớp 5 mà hihihi ;;;; nháy mắt
vì MN x PQ tại O nên \(\widehat{MOP}\)và \(\widehat{NOQ}\)là hai góc đối đỉnh (gt)
=> \(\widehat{MOP}=\widehat{NOQ}=\frac{160^0}{2}=80^0\)
p/s: đây là mk tự nghĩ -> tự làm, ok nếu sai cấm trách ko ns trc!

Tham khảo:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
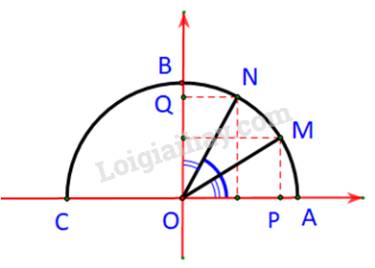
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)

Ta có: \(\widehat{MOP}+\widehat{NOP}=180^0\) (kề bù)
Mà: \(\widehat{MOP}=4.\widehat{NOP}\left(GT\right)\)
\(\Rightarrow4.\widehat{NOP}+\widehat{NOP}=180^0\)
\(\Rightarrow5.\widehat{NOP}=180^0\)
\(\Rightarrow\widehat{NOP}=180^0:5=36^0\)
\(\widehat{MOP}=4.\widehat{NOP}\left(GT\right)\)
\(\Rightarrow\widehat{MOP}=4.36^0=144^0\)
Có: \(\left\{{}\begin{matrix}\widehat{QOM}=\widehat{NOP}=36^0\\\widehat{NOQ}=\widehat{MOP}=144^0\end{matrix}\right.\) (đối đỉnh)

Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)

Bổ sug đề: Cho (O), BD,CE là các dây của (O)
Sửa đề: Chứng minh góc BOE=góc EDB+góc ECB
1/2(góc EDB+góc ECB)
=1/2(1/2sđ cung EB+1/2sđ cung EB)
=1/2sđ cung EB
=1/2*góc BOE
=>góc EDB+góc ECB=góc BOE

\(\widehat{AOD}=110^0\),\(\widehat{BOC}=110^0\),\(\widehat{BOD}=70^0\)