Bài 3: Tìm hai số a,b biết \(14a=12b\) và \(a+b=130\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
19 tháng 7 2019
2. Ta có: x - 3 = y(x - 2)
=> x - 3 - y(x - 2) = 0
=> (x - 2) - y(x - 2) = 1
=> (1 - y)(x - 2) = 1
=> 1 - y; x - 2 \(\in\)Ư(1) = {1; -1}
Lập bảng :
| 1 - y | 1 | -1 |
| x - 2 | 1 | -1 |
| y | 0 | 2 |
| x | 3 | 1 |
Vậy ...
CM
14 tháng 9 2018
Chọn B.
Phương pháp:
Giải phương trình bằng phương pháp xét hàm số.
Cách giải:
S
10 tháng 7 2019
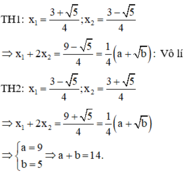
\(14a-7b+4=7\left(2a-b+1\right)-3⋮7̸\)\(\Rightarrow4a+2b+1⋮7\Leftrightarrow4a+21a+2b-14b+1+7⋮7\Leftrightarrow25a-12b+8⋮7\)
10 tháng 7 2019
\(14a-7b+4=7\times\left(2a-b\right)+4⋮̸7\)
\(\left(14a-7b+4\right)\left(4a+2b+1\right)⋮7\)
\(\Rightarrow4a+2b+1⋮7\)
\(21a-14b+7⋮7\)
\(\Rightarrow\left(4a+2b+1\right)+\left(21a-14b+7\right)⋮7\)
\(\Rightarrow\left(4a+21a\right)-\left(14b-2b\right)+\left(1+7\right)⋮7\)
\(\Rightarrow25a-12b+8⋮7\)
CM
4 tháng 2 2019
Đáp án C
Điều kiện 4 x 2 − 4 x + 1 2 x > 0 ⇔ x > 0
P T ⇔ log 7 2 x − 1 2 + 2 x − 1 2 = 2 x + log 7 2 x ⇔ f 2 x − 1 2 = f 2 x
với f t = log 7 t + t
f ' t = 1 t ln 7 + 1 > 0 với t >0
→ P T ⇔ 2 x = 2 x − 1 2 ⇔ x = 3 ± 5 4
⇒ x 1 + 2 x 2 = 9 ± 5 4 ⇒ a = 9 b = 5 ⇒ a + b = 14
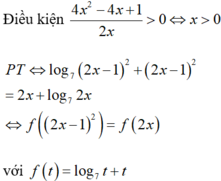
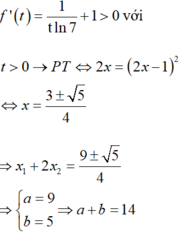
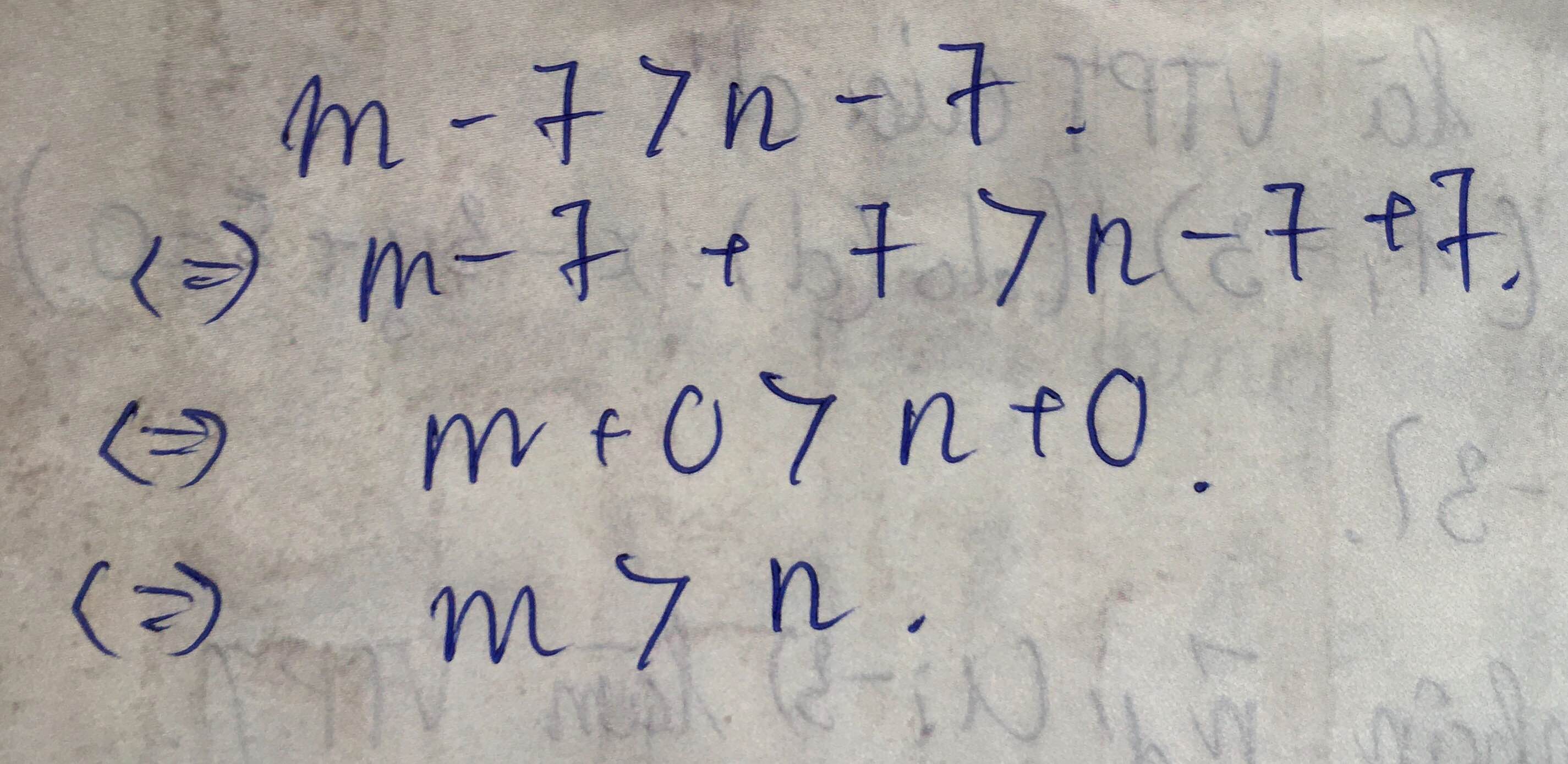
\(14a=12b\)\(\Rightarrow\frac{a}{12}=\frac{b}{14}\)
Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{a}{12}=\frac{b}{14}=\frac{a+b}{12+14}=\frac{130}{26}=5\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{12}=5\Rightarrow a=5.12=60\\\frac{b}{14}=5\Rightarrow b=5.14=70\end{cases}}\)
\(14a=12b\Rightarrow\frac{a}{12}=\frac{b}{14}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{a}{12}=\frac{b}{14}=\frac{a+b}{12+14}=\frac{130}{26}=5\)
\(\frac{a}{12}=5\Rightarrow a=60\)
\(\frac{b}{14}=5\Rightarrow b=70\)