Có bao nhiêu giá trị của m, m thuộc Z để y = -x3 - (2m-1)x2 - (m+3)x - m -1 đồng biến trên khoảng có độ dài không lớn hơn 2
A. 0 B. 1. C. 2. D. 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 6 2018
Chọn B
Phương pháp:
Tính y'.
Tìm m để 
Cách giải:
Ta có 
Xét phương trình y' = 0 
có 
Suy ra phương trình y' = 0 luôn có hai nghiệm 
Dễ thấy 
trong khoảng 
thì hàm số đồng biến.
Bài toán thỏa 
Do 
Vậy có 
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để 
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm 
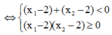
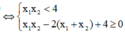
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)
CM
6 tháng 11 2017
Đáp án D
Cách giải:
+ 
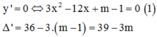
=> Hàm số đồng biến trên 
+ 
Phương trình (1) có 2 nghiệm phân biệt 
Theo đinh lí Viet ta có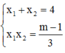 
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
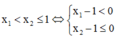
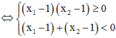
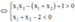
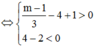( vô lí )
Vậy m ≥ 13
Mà 
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006
CM
15 tháng 7 2019
Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀ x ⇔ ∆ ' = 4m2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.
CM
22 tháng 8 2018
Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4 m 2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.
CM
8 tháng 2 2019
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 