Câu 2)
a) 3cos2x - 2cosx + 1= 0
b) 25sin2x +15sin2x + 9cos2x =25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
2 tháng 10 2019
25sin2x + 15sin2x + 9cos2x = 25
⇔ 25sin2x + 15.2sinx.cosx + 9cos2x – 25 = 0
⇔ 25.(sin2x – 1) + 15.2.sinx.cosx + 9cos2x = 0
⇔ -25.cos2x + 30sinx.cosx + 9cos2x = 0
⇔ 16.cos2x – 30.sinx.cosx = 0
⇔ 2.cosx.(8cosx – 15sinx) = 0
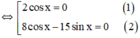
+ Giải (1): 2.cos x = 0 ⇔ cos x = 0
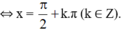
+ Giải (2): 8.cos x – 15.sin x = 0
⇔ 8.cos x = 15.sin x.
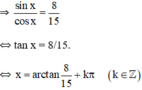
Vậy phương trình có tập nghiệm
HP
2 tháng 8 2021
\(\left(2cosx+1\right)\left(3cos2x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\3cos2x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cos2x=\dfrac{4}{3}>1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{2\pi}{3}+k2\pi\)
AH
Akai Haruma
Giáo viên
24 tháng 7 2020
m)
$\sin 4x-\cos ^4x=\cos x-2$
$\Leftrightarrow (\sin ^2x+\cos ^2x)(\sin ^2x-\cos ^2x)=\cos x-2$
$\Leftrightarrow \sin ^2x-\cos ^2x=\cos x-2$
$\Leftrightarrow 1-2\cos ^2x=\cos x-2$
$\Leftrightarrow 2\cos ^2x+\cos x-3=0$
$\Leftrightarrow (2\cos x+3)(\cos x-1)=0$
Nếu $2\cos x+3=0\Rightarrow \cos x=\frac{-3}{2}< -1$ (loại)
Nếu $\cos x-1=0\Rightarrow \cos x=1\Rightarrow x=2k\pi$ với $k$ nguyên
AH
Akai Haruma
Giáo viên
24 tháng 7 2020
k) ĐK:.......
$\tan ^25x=\frac{1}{3}\Rightarrow \tan 5x=\pm \sqrt{\frac{1}{3}}$
$\Rightarrow 5x=k\pi +\tan ^{-1}\frac{\pm 1}{\sqrt{3}}$
$\Rightarrow x=frac{k}{5}\pi +\tan ^{-1}\frac{\pm 1}{\sqrt{3}}$ với $k$ nguyên.
Số đẹp hơn thì có thể giải như sau:
$PT \Leftrightarrow \frac{\sin ^25x}{\cos ^25x}=\frac{1}{3}$
$\Rightarrow 3\sin ^25x=\cos ^25x$
$\Rightarrow 4\\sin ^25x=1\Rightarrow \sin 5x=\pm \frac{1}{2}$
$\Rightarrow x=\frac{k\pi}{5}\pm \frac{\pi}{30}$ với $k$ nguyên.
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 12 2018
\(2cosx+3sinx+\dfrac{1}{3}cos2x-sin2x=\dfrac{8}{3}\)
\(\Leftrightarrow6cosx+9sinx+cos2x-3sin2x-8=0\)
\(\Leftrightarrow6cosx-6sinx.cosx+9sinx-9+1+1-2sin^2x=0\)
\(\Leftrightarrow6cosx\left(1-sinx\right)-9\left(1-sinx\right)+2\left(1-sinx\right)\left(1+sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx-9+2+2sinx=0\right)\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx+2sinx-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}1-sinx=0\\6cosx+2sinx=7\end{matrix}\right.\)
TH1: \(1-sinx=0\Rightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
TH2: \(6cosx+2sinx=7\) (1)
Do \(6^2+2^2=40< 7^2=49\Rightarrow\) pt (1) vô nghiệm
Vậy pt đã cho có nghiệm \(x=\dfrac{\pi}{2}+k2\pi\)
HP
28 tháng 8 2021
1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
HP
28 tháng 8 2021
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2019
a/ \(\Leftrightarrow sin8x+sin2x=sin12x+sin2x\)
\(\Leftrightarrow sin12x=sin8x\)
\(\Rightarrow\left[{}\begin{matrix}12x=8x+k2\pi\\12x=\pi-8x+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{\pi}{20}+\frac{k\pi}{10}\end{matrix}\right.\)
b/ \(\sqrt{2}sinx-2\sqrt{2}cosx-2+2sinx.cosx=0\)
\(\Leftrightarrow\sqrt{2}sinx\left(\sqrt{2}cosx+1\right)-2\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}sinx-2\right)\left(\sqrt{2}cosx+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\sqrt{2}>1\left(l\right)\\cosx=-\frac{\sqrt{2}}{2}\end{matrix}\right.\) \(\Rightarrow x=\pm\frac{3\pi}{4}+k2\pi\)
c/ Không là hệ quả của pt nào, chắc bạn ghi nhầm đề bài
HP
20 tháng 9 2021
\(3cos^2x-2sinx+2=0\)
\(\Leftrightarrow-3\left(1-cos^2x\right)-2sinx+5=0\)
\(\Leftrightarrow3sin^2x+2sinx-5=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(3sinx+5\right)=0\)
\(\Leftrightarrow sinx=1\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
1 tháng 10 2021
a
\(\Leftrightarrow\left(3sinx-sin3x\right)cos3x+\left(3cosx+cos3x\right)sin3x+3\sqrt{3}cos4x=3\)
\(\Leftrightarrow\left(sinx.cos3x+sin3x.cosx\right)+\sqrt{3}cos4x=1\)
\(\Leftrightarrow sin4x+\sqrt{3}cos4x=1\)
Tới đây thôi, mình lười ghi rồi =))
b
\(\Leftrightarrow\left(1-cos2x\right)\left(2sin^2x-1\right)\left(2sin^2+1\right)=cos2x\left(7cos^22x+3cos2x-4\right)\)
\(\Leftrightarrow\left(1-cos2x\right)\left(-cos2x\right)\left(2-cos2x\right)=cos2x\left(7cos^22x+3cos2x+4\right)\)
\(\Leftrightarrow-cos^22x+3cos2x-2=7cos^22x+3cos2x+4\)
\(\Leftrightarrow4cos^22x+3=0\)
=> pt vô nghiệm
a/ Cái đầu tiên vô nghiệm rồi :v
b/ \(\Leftrightarrow\left(5\sin x\right)^2+5.3.2\sin x\cos x+\left(3\cos x\right)^2=25\)
\(\Leftrightarrow\left(5\sin x+3\cos x\right)^2=25\Leftrightarrow\left[{}\begin{matrix}5\sin x+3\cos x=5\\5\sin x+3\cos x=-5\end{matrix}\right.\)
Xét \(5\sin x+3\cos x=5\)
\(\cos\frac{x}{2}=0\Rightarrow x=\pi+k2\pi\)
\(\cos\frac{x}{2}\ne0\Leftrightarrow x\ne\pi+k2\pi\)
Đặt \(t=\tan\frac{x}{2}\Rightarrow\left\{{}\begin{matrix}\sin x=\frac{2t}{1+t^2}\\\cos x=\frac{1-t^2}{1+t^2}\end{matrix}\right.\)
\(\Rightarrow5\frac{2t}{1+t^2}+3.\frac{1-t^2}{1+t^2}=5\)
\(\Leftrightarrow8t^2-10t+2=0\) <tự giải nha, trường hợp 2 tương tự :)>