Tìm n biết
a) (1/3)^2n-1=243
b) (0,125)^n+1=64
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 5 chia hết cho n - 1 khi n - 1 là ước của 5
Ư(5) = {-5; -1; 1; 5}
⇒n - 1 ∈ {-5; -1; 1; 5}
Do n là số tự nhiên nên
n ∈ {0; 2; 6}
b) Do n là số tự nhiên nên 2n + 1 > 0
20 chia hết cho 2n + 1
⇒2n + 1 ∈ Ư(20) = {1; 2; 4; 5; 10; 20}
⇒2n ∈ {0; 3; 5; 6; 11; 21}
Lại do n là số tự nhiên
⇒n ∈ {0; 3}

a,\(\left(\dfrac{1}{3}\right)^{2n-1}=243\)
\(\Rightarrow\left(\dfrac{1}{3}\right)^{2n-1}=\left(\dfrac{1}{3}\right)^{-5}\)
Vì \(\dfrac{1}{3}\ne\pm1;\dfrac{1}{3}\ne0\) nên
\(2n-1=-5\Rightarrow2n=-4\Rightarrow n=-2\)
Vậy........
b, \(\left(0,125\right)^{n+1}=64\)
\(\Rightarrow\left(\dfrac{1}{8}\right)^{n+1}=\left(\dfrac{1}{8}\right)^{-2}\)
Vì \(\dfrac{1}{8}\ne\pm1;\dfrac{1}{8}\ne0\) nên
\(n+1=-2\Rightarrow n=-3\)
Vậy..........
Chúc bạn học tốt!!!
a) Ta có: \(\left(\dfrac{1}{3}\right)^{2n-1}=243\Rightarrow\left(3^{-1}\right)^{2n-1}=3^5\)
\(\Rightarrow3^{-2n+1}=3^5\)
Suy ra: \(-2n+1=5\Rightarrow-2n=4\Rightarrow n=-2\)
b) \(\left(0,125\right)^{n+1}=64\Rightarrow\left(\dfrac{1}{8}\right)^{n+1}=8^2\)
\(\Rightarrow\left(8^{-1}\right)^{n+1}=8^2\)
\(\Rightarrow8^{-n-1}=8^2\)
Suy ra: \(-n-1=2\Rightarrow n=-3\)
Hok tốt

a, 3 n . 3 = 243 => 3 n + 1 = 243 => 3 n + 1 = 3 5
=> n + 1 = 5 => n = 4
Vậy n = 4
b, 4 3 . 2 n + 1 = 1
=> 2 2 3 . 2 n + 1 = 1
=> 2 2 . 3 . 2 n + 1 = 1 => 2 6 . 2 n + 1 = 1
=> 2 6 + n + 1 = 1 => 2 n + 7 = 2 0
=> n + 7 = 0
Không tìm được số tự nhiên n thỏa mãn đầu bài
c, 2 n - 15 = 17
=> 2 n = 32 => 2 n = 2 5
=> n = 5
Vậy n = 5
d, 8 ≤ 2 n + 1 ≤ 64
=> 2 3 ≤ 2 n + 1 ≤ 2 6
=> 3 ≤ n + 1 và n+1 ≤ 6
=> 2 ≤ n và n ≤ 5
=> 2 ≤ n ≤ 5
Vậy 2 ≤ n ≤ 5
e, 9 < 3 n < 243
=> 3 2 < 3 n < 3 5
=> 2<n<5
Vậy 2<n<5

Bài 1:
a. Gọi d là ƯCLN(n+2, n+3). Khi đó:
$n+2\vdots d; n+3\vdots d$
$\Rightarrow (n+3)-(n+2)\vdots d$
Hay $1\vdots d$
$\Rightarrow d=1$. Vậy $ƯCLN(n+2, n+3)=1$ nên hai số này nguyên tố cùng nhau.
b.
Gọi $d=ƯCLN(2n+1, 9n+4)$
$\Rightarrow 2n+1\vdots d; 9n+4\vdots d$
$\Rightarrow 9(2n+1)-2(9n+4)\vdots d$
Hay $1\vdots d$
$\Rightarrow d=1$. Vậy $ƯCLN(2n+1, 9n+4)=1$ nên hai số này nguyên tố cùng nhau.
Bài 2:
a. Vì ƯCLN(a,b)=24 nên đặt $a=24x, b=24y$ với $x,y$ là 2 số nguyên tố cùng nhau.
Khi đó: $a+b=24x+24y=192$
$\Rightarrow 24(x+y)=192$
$\Rightarrow x+y=8$
Vì $(x,y)$ nguyên tố cùng nhau nên $(x,y)=(1,7), (3,5), (5,3), (1,7)$
$\Rightarrow (a,b)=(24,168), (72, 120), (120,72), (168,24)$

a: =>n-4 thuộc Ư(15)
mà n thuộc N
nên n-4 thuộc {-3;-1;1;3;5;15}
=>n thuộc {1;3;5;7;9;19}
b: =>2n-4+9 chia hết cho n-2
=>n-2 thuộc {1;-1;3;-3;9;-9}
mà n>=0
nên n thuộc {3;1;5;11}
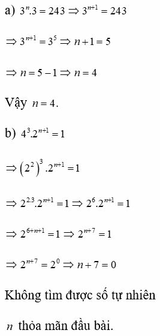
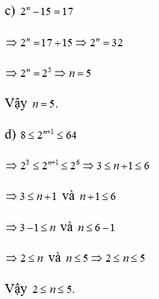
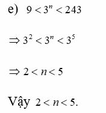
\(\frac{1}{3}^{2n-1}=243\)
\(< =>\frac{1}{3}^{n+n}=\frac{243}{3}=81\)
\(< =>\frac{1}{3^{n+n}}=81\)
\(< =>81.3^n.3^n=1\)
\(< =>3^{2n}=\frac{1}{81}\)
\(< =>3^{2n}=3^{-4}\)
\(< =>x=-2\)
Bài làm:
a) \(\left(\frac{1}{3}\right)^{2n-1}=243\)
\(\Leftrightarrow3^{1-2n}=3^5\)
\(\Rightarrow1-2n=5\)
\(\Leftrightarrow2n=-4\)
\(\Rightarrow n=-2\)
b) \(\left(0,125\right)^{n+1}=64\)
\(\Leftrightarrow\left(\frac{1}{8}\right)^{n+1}=8^2\)
\(\Rightarrow-n-1=2\)
\(\Rightarrow n=-3\)