Giải phương trình: sin5x-sin3x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 11 2017
sin3x + sin5x = 0
⇔ 2sin4x. cosx = 0
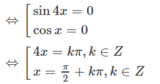
Vậy nghiệm của phương trình là:
TD
17
SG
1
17 tháng 5 2017
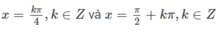
\(4\sin3x+\sin5x-2\sin x\cos2x=0\)
\(\Leftrightarrow\)\(4\sin3x+\sin5x-\sin3x+\sin x=0\)
\(\Leftrightarrow3\sin3x+\sin5x+\sin x=0\)
\(\Leftrightarrow3\sin3x+2\sin3x\cos2x=0\)
\(\Leftrightarrow\sin3x\left(3+2\cos2x\right)=0\)
Đáp số : \(x=k\dfrac{\pi}{3},k\in\mathbb{Z}\)
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 11 2019
\(cosx+cos3x+cos2x+cos4x=0\)
\(\Leftrightarrow2cos2x.cosx+2cos3x.cosx=0\)
\(\Leftrightarrow cosx.\left(cos2x+cos3x\right)=0\)
\(\Leftrightarrow cosx.cos\frac{5x}{2}.cos\frac{x}{2}=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cos\frac{5x}{2}=0\\cos\frac{x}{2}=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\\frac{5x}{2}=\frac{\pi}{2}+k\pi\\\frac{x}{2}=\frac{\pi}{2}+k\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{5}+\frac{k2\pi}{5}\\x=\pi+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 11 2019
\(sinx+sin7x+sin3x+sin5x=0\)
\(\Leftrightarrow2sin4x.cos3x+2sin4x.cosx=0\)
\(\Leftrightarrow sin4x\left(cos3x+cosx\right)=0\)
\(\Leftrightarrow sin4x.cos2x.cosx=0\)
\(\Leftrightarrow sin4x=0\)
\(\Rightarrow4x=k\pi\Rightarrow x=\frac{k\pi}{4}\)
Lý do chỉ cần 1 pt sin4x=0 do sin4x bao hàm cả cosx và cos2x ở trong đó
CM
19 tháng 5 2018
Đáp án B
PT: sin 5 x + sin 3 x = sin 4 x
⇔ 2 sin 4 x cos x − sin 4 x = 0 ⇔ sin 4 x 2 cos x − 1 = 0
⇔ sin 4 x = 0 cos x = 1 2 ⇔ x = k π 4 1 x = − π 3 + 2 k π 2 x = π 3 + 2 k π 3
Trong đoạn − π 2 ; π 2 thì số nghiệm của (1) là 5 ứng với k ∈ 0 ; ± 1 ; ± 2 , (2) là 1 ứng với k = 0 , (3) là 1 ứng với k=0.
Như vậy PT đã cho có 7 nghiệm trong đoạn − π 2 ; π 2 .
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
\(\Leftrightarrow sin5x=-sin3x\)
\(\Leftrightarrow sin5x=sin\left(-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=-3x+k2\pi\\5x=\pi+3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}8x=k2\pi\\2x=\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{4}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\))
CM
6 tháng 3 2018
4sin3x + sin5x – 2sinx.cos2x = 0
⇔ 4sin3x + sin5x – sin3x + sinx = 0
⇔ 3sin3x + sin5x + sinx = 0
⇔ 3sin3x + 2sin3x.cos2x = 0
⇔ sin3x(3 + 2cos2x) = 0.
Đáp số: x = kπ/3, k ∈ Z.