cho tam giác abc vuông tại a có ab=7cm, ac=24 cm tính độ dài đường trung tuyến am
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12

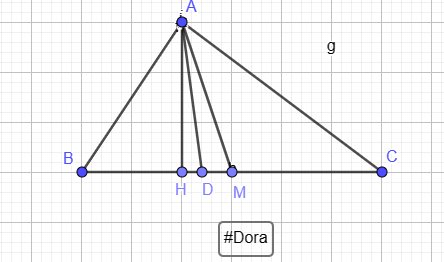
Vì `\triangle ABC` vuông tại `A` có `AM` là đường trung tuyến
`=>AM=MC=1/2BC =>BC =40(cm)`
`@` Xét `\triangle ABC` vuông tại `A` có: `AC=\sqrt{BC^2 -AB^2}=32(cm)` (Py-ta-go)
`@` Mặt khác: Ta có `AH` là đường cao
`=>BH=[AB^2]/[BC]` (Ht giữa cạnh và đường cao)
`=>BH =14,4(cm)`
`@` Ta có: `HM =BC-BH-MC=5,6(cm)`

Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=12\left(cm\right)\)
Do AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{25}{2}=12,5\left(cm\right)\)
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=225+400=625\Rightarrow BC=25\)cm
Xét tam giác ABC, đường cao AH
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{300}{25}=12\)cm
Vì AM là đường trung tuyến suy ra : \(AM=\dfrac{BC}{2}=\dfrac{25}{2}\)cm

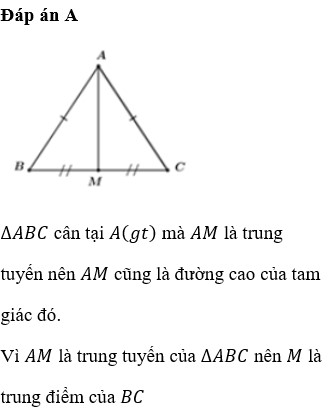
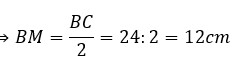
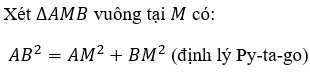
Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Vì AM là tt ứng ch nên \(AM=\dfrac{1}{2}BC=\dfrac{25}{2}\left(cm\right)\)
Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{7^2+24^2}=25$ (cm)
Đối với tam giác vuông thì độ dài đường trung tuyến ứng với cạnh huyền bằng 1 nửa cạnh huyền
CM tính chất trên bạn có thể tham khảo tại đây:
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-vuong-tai-a-m-la-trung-diem-cua-bc-chung-minh-bc-2am-minh-chua-hoc-3939tinh-chat-duong-trung-tuyen-trong-tam-giac-vuong3939-nen-giai-bth-giup-mik-a.2592190724387
Vậy $ AM=\frac{BC}{2}=12,5$ (cm)