Giúp mình vs 😭😭
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



refer
1.T 2.F
3.T 4.F
5.F 6.F
7.T 8.T
1.He lives in Los Angeles California.
2.His sister's name Emma.
3.He wake up at about half past seven.
4.Yes,he does.
5.He leaves home at a quarter to eight.
6.He has lunch at school.
7.He returns home at a quarter past five after school.
8.He makes his homework at home.
9.Yes,he is.

Câu 5:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(c5\) \(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\left(đpcm\right)\)
\(c4:\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GG'}\)
\(\overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=\overrightarrow{GG'}\)\(\Leftrightarrow\overrightarrow{G'A}+\overrightarrow{AA'}+\overrightarrow{G'B}+\overrightarrow{B'B}+\overrightarrow{G'C}+\overrightarrow{CC'}=\overrightarrow{GG'}\)
\(\Leftrightarrow\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=3\overrightarrow{GG'}\)\(\left(dpcm\right)\)
\(c3:a,\) \(2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IA}+2\overrightarrow{IM}=2\overrightarrow{MI}+2\left(\overrightarrow{IM}+\overrightarrow{MI}\right)=2.\overrightarrow{0}=\overrightarrow{0}\left(đpcm\right)\)
\(b,2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(=2\left(\overrightarrow{OI}+\overrightarrow{IA}\right)+\overrightarrow{OI}+\overrightarrow{IB}+\overrightarrow{OI}+\overrightarrow{IC}\)
\(=4\overrightarrow{OI}+2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\)\(=4\overrightarrow{OI}+\overrightarrow{0}=4\overrightarrow{OI}\left(đpcm\right)\)
\(c2:\) \(\left\{{}\begin{matrix}3AH=2AB\\3AK=AC\\4BM=3MC\\\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{3}{2}\overrightarrow{AH}\\\overrightarrow{AC}=3\overrightarrow{AK}\\\overrightarrow{BM}=\dfrac{3}{7}\overrightarrow{BC}\Rightarrow\overrightarrow{BC}=\dfrac{7}{3}\overrightarrow{BM}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=3\overrightarrow{AK}-\dfrac{3}{2}\overrightarrow{AH}\)
\(\Rightarrow\dfrac{7}{3}\overrightarrow{BM}=3\overrightarrow{AK}-\dfrac{3}{2}\overrightarrow{AH}\Leftrightarrow\overrightarrow{BM}=\dfrac{9}{7}\overrightarrow{AK}-\dfrac{9}{14}\overrightarrow{AH}\)


Câu 7
a,Xét \(\Delta ICA\) và \(\Delta ICB\) ta có :
\(AC=CB\) ( do \(\Delta ABC\) cân tại \(C\) nên 2 cạnh bên bằng nhau )
\(\widehat{CAI} = \widehat{CBI}\) ( hai góc ở đáy )
\(AI=IB \)(do \(I\) là trung điểm của \(AB\))
\(\Rightarrow\Delta ICA=\Delta ICB\left(c.g.c\right)\)
b,Ta có \(CI \) là trung tuyến suất phát từ đỉnh \(C\)
\(\Rightarrow CI\perp AB\)(tính chất đường trung tuyến trong tam giác cân)
c, Áp dụng định lý \(Pi-ta-go\) vào tam giác vuông \(CIA\) ta có :
\(AC^2=CI^2+IA^2\Rightarrow AC=\sqrt{CI^2+IA^2}\)
\(\Leftrightarrow AC=\sqrt{12^2+5^2}=13\)
\(\Rightarrow AC=BC=13\left(cm\right)\)
Chu vi \(\Delta ABC\) là
\(AC+CB+AB=13+13+10=36\left(cm\right)\)

Câu 1:
1: \(\overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\overrightarrow{OD}}{2}=\dfrac{\overrightarrow{BO}+\overrightarrow{OA}}{2}=\dfrac{\overrightarrow{BA}}{2}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
\(\overrightarrow{BD}=2\cdot\overrightarrow{BO}=-2\cdot\overrightarrow{OB}\)
nên y=-2
2: \(2\cdot\overrightarrow{ON}=\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{DO}+\overrightarrow{OC}=\overrightarrow{DC}=\overrightarrow{AB}\)
Vậy: Các vecto u thỏa mãn là vecto DC và vecto AB

Hoàng Hoa Thám (tên thật: Trương Văn Thám)( 1858 - 1913), người lãnh đạo cuộc Khởi nghĩa Yên Thế (1885 - 1913) chống Pháp. Quê làng Dị Chế, huyện Tiên Lữ, tỉnh Hưng Yên; di cư lên Sơn Tây (Hà Tây), rồi đến Yên Thế (Bắc Giang). Năm 1885, tham gia khởi nghĩa của Cai Kinh (Hoàng Đình Kinh) ở Lạng Giang. Sau khi Cai Kinh chết, Đề Thám tiếp tục hoạt động, lập căn cứ ở Yên Thế và trở thành thủ lĩnh danh tiếng nhất của phong trào nông dân chống Pháp. Trong gần 30 năm lãnh đạo đã tổ chức đánh nhiều trận, tiêu biểu là các trận ở thung lũng Hố Chuối (12.1890) và Đồng Hom (2.1892). Pháp phải hai lần giảng hoà với Đề Thám vào năm 1894 và 1897. Những năm 1898 - 1908, xúc tiến việc xây dựng Phồn Xương thành căn cứ kháng chiến, đồng thời bí mật liên hệ với lực lượng yêu nước ở bên ngoài. Nhiều sĩ phu như Phan Bội Châu, Phan Chu Trinh, Phạm Văn Ngôn, Lê Văn Huân, Nguyễn Đình Kiên... đã gặp gỡ Hoàng Hoa Thám và bàn kế hoạch phối hợp hành động. Đầu 1909, Pháp mở cuộc tấn công quy mô lớn nhằm tiêu diệt nghĩa quân. Đề Thám vừa tổ chức đánh trả, vừa phải rút lui khỏi Yên Thế, đến Thái Nguyên, Tam Đảo. Lực lượng nghĩa quân giảm sút dần và tới cuối 1909 bị tan rã. Đề Thám phải sống ẩn náu trong núi rừng Yên Thế. Bị tay sai của Pháp sát hại 10.2.1913.


\(12.\left(x-1\right)=0\)
\(x-1=0:12\)
\(x-1=0\)
\(x=0+1\)
\(x=1\)

d: ta có: \(C=3+3^3+3^5+...+3^{1991}\)
\(=3\left(1+3^2+3^4\right)+...+3^{1987}\left(1+3^2+3^4\right)\)
\(=91\cdot\left(3+...+3^{1987}\right)⋮13\)







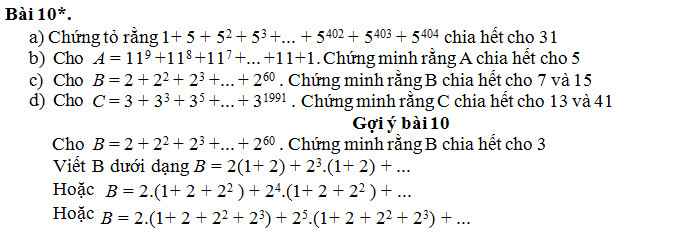
giúp j cơ