Cho điểm M bất kì nằm trong tam giác ABC. Chứng minh \(\widehat{BMC}>\widehat{BAC}\)
Cần gấp ạ, mai nộp ròi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://olm.vn/hoi-dap/detail/228905523575.html

Ta cần hai bổ đề:
Bổ đề 1: (Hình bên phải) Xét tứ giác MNPQ nội tiếp (QN). Trên MQ và NP lấy S,T sao cho ^MNS = ^PQT. Khi đó MP chia đôi ST.
Thật vậy: Gọi NS,QT cắt (QN) tại điểm thứ hai lần lượt là K,L. KL cắt MP tại I
Áp dụng ĐL Pascal cho bộ 6 điểm Q,K,M,N,L,P ta được 3 điểm S,I,T thẳng hàng
Ta có ^MNK và ^PQL là hai góc nội tiếp, ^MNK = ^PQL nên (MK = (PL
Từ đó dựng \(\Delta\)PRL vào phía trong đường tròn sao cho \(\Delta\)PRL = \(\Delta\)KSM
Vì tứ giác MKPL là hình thang cân nên IS = IR (Tính đối xứng)
Ta thấy ^IPT = ^MKS (Cùng chắn cung MN) = ^LPR. Tương tự ^PLT = ^ILR
Suy ra T và R là hai điểm Đẳng giác trong \(\Delta\)PIL => ^RIP = ^TIL
Ta lại có ^PTL = ^KSM = ^PRL ( = 900 + ^MNK = 900 + ^PQL) => Tứ giác TRPL nội tiếp
Từ đó có biến đổi góc: ^IRT = 3600 - ^IRP - ^PRT = ^RIP + ^RPI + ^TLP = ^TIL + ^TRL + ^ILR = ^ITL
=> \(\Delta\)TIR cân tại I => IT = IR = IS. Tức là MP đi qua trung điểm I của ST.
Bổ đề 2: (Hình bên trái) Xét 2 góc ^ACB và ^ADB cùng nhìn đoạn AB dưới một góc không đổi (C và D nằm khác phía so với AB). Kẻ AE,BF vuông góc với BC,AD. Khi đó EF chia đôi CD.
Chứng minh: Gọi H,K lần lượt là trực tâm của \(\Delta\)ABC và \(\Delta\)ABD. Do ^ACB và ^ADB cùng nhìn AB dưới một góc không đổi nên tâm ngoại tiếp của \(\Delta\)ABC và \(\Delta\)ADB đối xứng nhau qua AB. Theo một kết quả quen thuộc thì CH = DK.
Suy ra tứ giác CHDK là hình bình hành, trung điểm của HK và CD trùng nhau (1)
Chú ý tứ giác AEBF nội tiếp (AB), ^EBH = ^FAK. Áp dụng Bổ đề 1 ta được EF chia đôi HK (2)
Từ (1) và (2) suy ra EF cũng chia đôi CD.
Giải bài toán:
Gọi O là tâm của hình thoi ABCD. Từ P,Q lần lượt kẻ PM,QN vuông góc với CQ,AP.
Ta thấy ^PAQ và ^PCQ cùng nhìn đoạn PQ dưới một góc không đổi bằng 1/2.^DAB
Đồng thời có PM vuông góc CQ, QN vuông góc AP. Áp dụng Bổ đề 2 ta thu được MN chia đôi AC
Hay MN đi qua O. Mặt khác ta có: \(\Delta\)CMP ~ \(\Delta\)COB (g.g) => \(\Delta\)CMO ~ \(\Delta\)CPB (c.g.c)
Suy ra ^CBP = ^COM = ^AON (Vì lúc này ^AON và ^COM đối đỉnh). Tương tự ^AON = ^ADQ
Từ đó ^CBP = ^ADQ. Kết hợp với BC // AD suy ra BP // DQ (đpcm).

a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{BAM}=\widehat{CAM}\)(AM là tia phân giác của \(\widehat{BAC}\))
AM chung
Do đó: ΔABM=ΔACM(c-g-c)
a) Ta có: ΔABM=ΔACM(cmt)
nên MB=MC(Hai cạnh tương ứng)
Xét ΔMBC có MB=MC(cmt)
nên ΔMBC cân tại M(Định nghĩa tam giác cân)

a) (thay vô y như toán đại í )
t.g OBC có: O1^+B1^+C1^=180 độ => O1^=180 độ - B^1-C1^
t.g ABC có: A1^+B2^+B^1+C^2+C1^=180 độ
=> A1^+B^2+C^2=180 độ - B^1-C^1=O1^
=> BOC^=BAC^+ABO^+ACO^
b) B2^+C2^=90 độ - A1^:2
=> B2^+C^2= 90 độ - (180 độ - B1^ - B2^ - C1^ - C2^):2
=> B2^+C2^= 90 độ - 90 độ +(B1^+B2^+C2^+C1^):2
=> B2^+C2^=B2+(C1^+C2^):2 ( vì BO là tia p.g của ABC^)
=> C2^=(C1^+C2^):2 => CO là tia p/g của ACB^

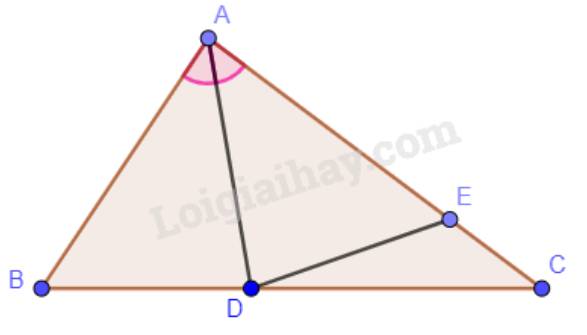
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).
Tam giác ABC có:
\(\widehat{BAC}+(\widehat{ABC}+\widehat{ ACB})=180^0\)
Tam giác MBC có:
\(\widehat{MBC}+(\widehat{MBC}+\widehat{MCB})=180^0\)
=> \(\widehat{BAC}+(\widehat{ABC}+\widehat{ ACB})=180^0 =\)\(\widehat{MBC}+(\widehat{MBC}+\widehat{MCB})=180^0\) (1)
Vì M nằm trong tam giác ABC nên tia BM nằm giữa hai tia BA và BC
=>\(\widehat{ABC}>\widehat{MBC}\)
Tương tự ta được : \(\widehat{ACB}=\widehat{ MCB}\)
=> \(\widehat{ABC}+\widehat{ACB}>\widehat{MBC}+\widehat{MCB}\) (2)
Từ (1) và (2) => \(\widehat{BMC}> \widehat{BAC}\)