cho ptr 7x2+2 (m-1)x -m2 = 0
a) tính m để ptr có nghiệm
b) tính tổng các bình phương 2 nghiệm của ptr theo m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2023
Δ=(2m-2)^2-4(m^2+m-2)
=4m^2-8m+4-4m^2-4m+8
=-12m+12
Để phương trình có hai nghiệm thì -12m+12>=0
=>m<=1
x1^2=6-x2^2-x1x2
=>(x1+x2)^2-2x1x2+x1x2=6
=>(x1+x2)^2-x1x2=6
=>(2m-2)^2-2(m^2+m-2)-6=0
=>4m^2-8m+4-2m^2-2m+4-6=0
=>2m^2-10m+2=0
=>\(m=\dfrac{5\pm\sqrt{21}}{2}\)
HY
13 tháng 3 2020
a.Thay \(x=1\) vào phương trình \(x^3+ax^2-4x-4=0\) , ta có:
\(1^3+a.1^2-4.1-4=0\\ \Leftrightarrow1+a-4-4=0\\\Leftrightarrow a-7=0\\\Leftrightarrow a=7\)
Vậy \(a=7\) để phương trình \(x^3+ax^2-4x-4=0\) có nghiệm \(x=1\)
b. Thay \(a=7\) vào phương trình \(x^3+ax^2-4x-4=0\) ta có:
\(x^3+7x^2-4x-4=0\\\Leftrightarrow x^3-x^2+8x^2-8x+4x-4=0\\ \Leftrightarrow x^2\left(x-1\right)+8x\left(x-1\right)+4\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^2+8x+4\right)=0\\\Leftrightarrow \left(x-1\right)\left(x+4-2\sqrt{3}\right)\left(x+4+2\sqrt{3}\right)=0\\\Leftrightarrow \left[{}\begin{matrix}x-1=0\\x+4-2\sqrt{3}=0\\x+4+2\sqrt{3}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-4+2\sqrt{3}\\x=-4-2\sqrt{3}\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là \(S=\left\{1;-4+2\sqrt{3};-4-2\sqrt{3}\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
Pt có 2 nghiệm pb khi \(\Delta'=1-\left(m-3\right)>0\Rightarrow m< 4\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
\(x_1^2-2x_2+x_1x_2=-12\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)-2x_2=-12\)
\(\Leftrightarrow2x_1-2x_2=-12\)
\(\Leftrightarrow x_1-x_2=-6\)
Kết hợp \(x_1+x_2=2\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1-x_2=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-2\\x_2=4\end{matrix}\right.\)
Thế vào \(x_1x_2=m-3\)
\(\Rightarrow m-3=-8\Rightarrow m=-5\) (thỏa mãn)
13 tháng 4 2023
Δ=(2m-2)^2-4(m+1)
=4m^2-8m+4-4m-4
=4m^2-12m
Để phương trình co hai nghiệm thì 4m^2-12m>0
=>m>3 hoặc m<0
x1/x2+x2/x1=4
=>x1^2+x2^2=4x1x2
=>(x1+x2)^2-2x1x2=4x1x2
=>(2m-2)^2-6(m+1)=0
=>4m^2-8m+4-6m-6=0
=>4m^2-14m-2=0
=>\(m=\dfrac{7\pm\sqrt{57}}{2}\)
9 tháng 4 2018
a)
(pt1) ; 2k +1 =5 => k =2
(pt2): 2 -1 = vậy k =2 nhận
b)
hệ có nghiệm duy nhất; <=> k khác -1
CM
16 tháng 1 2017
a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: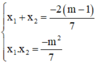 
Khi đó:
S
1
30 tháng 3 2023
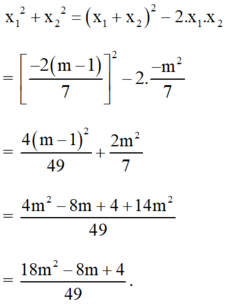
Δ=(2m+1)^2-4(m^2+m)
=4m^2+4m+1-4m^2-4m=1>0
=>PT luôn có 2 nghiệm pb
-2<x1<x2<4
=>-4<x1+x2<8
=>-4<2m+1<8
=>-5<2m<7
=>-5/2<m<7/2
\(\Delta'=\left(m-1\right)^2+7m^2=8m^2-2m+1=8\left(m-\frac{1}{8}\right)^2+\frac{7}{8}>0;\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
Theo Viet \(\left\{{}\begin{matrix}x_1+x_2=\frac{-2\left(m-1\right)}{7}\\x_1x_2=-\frac{m^2}{7}\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\frac{4\left(m-1\right)^2}{49}+\frac{2m^2}{7}=\frac{18m^2-8m+4}{7}\)