Cho tam giác ABC cân tại A, đường cao BH. Trên đáy BC lấy điểm M, vẽ MD⊥AB , ME⊥AC, MF⊥BH. a. Chứng minh ME=FH b, Chứng minh tam giác DBM= tam giác FMB c, Chứng minh khi M chạy trên BC thì tổng MD+ME có giá trị không đổi. d, Trên tia đối của tia CA lấy điểm K sao cho KC=EH. Chứng minh rằng trung điểm của KD nằm trên cạnh BC. Làm theo cách lớp 7 nhá...
Đọc tiếp
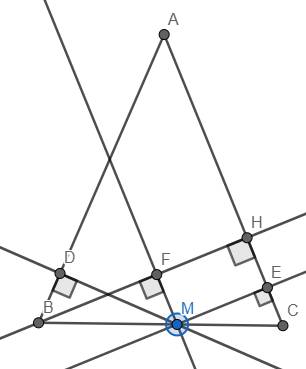
Cho tam giác ABC cân tại A, đường cao BH. Trên đáy BC lấy điểm M, vẽ MD⊥AB , ME⊥AC, MF⊥BH.
a. Chứng minh ME=FH
b, Chứng minh tam giác DBM= tam giác FMB
c, Chứng minh khi M chạy trên BC thì tổng MD+ME có giá trị không đổi.
d, Trên tia đối của tia CA lấy điểm K sao cho KC=EH. Chứng minh rằng trung điểm của KD nằm trên cạnh BC.
Làm theo cách lớp 7 nhá :))
a, Xét hình tứ giác MEHF. Ta có các góc \(\widehat{MFH}\)\(\widehat{FHE}\),\(\widehat{H}EM\)là góc vuông .Vì vậy MEHF là hình chữ nhật. Suy ra ME=FH
b, Tam giác DBM và FMB là tam giác vuông có chung cạch huyền BM. Vì vậy để chứng minh 2 tam giác bằng nhau ta chỉ cần chứng mình góc \(\widehat{DBM}\)= \(\widehat{BMF}\)?
Thật vậy, theo đề FM//AC=> \(\widehat{BMF}\)=\(\widehat{BCA}\)
Mặt khác \(\Delta ABC\)cân tại A nên \(\widehat{BCA}\)= \(\widehat{DBM}\)
Do vậy góc \(\widehat{DBM}\)= \(\widehat{BMF}\)hay:\(\Delta DBM\)=\(\Delta FMB\)
c. Do \(\Delta DBM\)=\(\Delta FMB\), nên MD = BF.
Đồng thời MFHE là hình chữ nhật nên ME=FH.
Suy ra: MD+ME=BF+FH=BH=const
d. Gọi N là giao điểm của DK và BC. Kẽ đường thẳng từ D song song với AC cắt BC tại O.
Xét \(\Delta NDO\)và \(\Delta NKC\)
Có DO//CK vì vậy \(\widehat{DON}\)=\(\widehat{NCK}\)và \(\widehat{ODN}\)=\(\widehat{CKN}\)
Đồng thời tam giác \(\Delta BDO\)cân tại D, nên BD=DO.
BD=MF do 2 tam giác\(\Delta DBM\)=\(\Delta FMB\)
FM=HE do MEHF là hình chữ nhật,
Theo đề CK=HE nên CK=DO. Suy ra \(\Delta NDO\)= \(\Delta NKC\). Vậy DN=ND hay N là trung điểm của DK