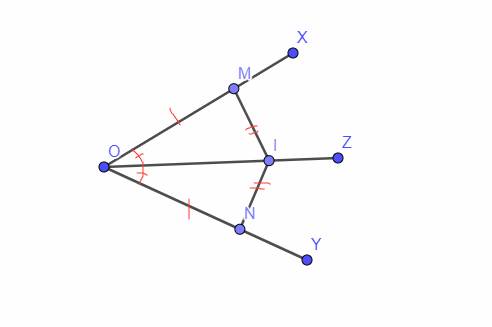
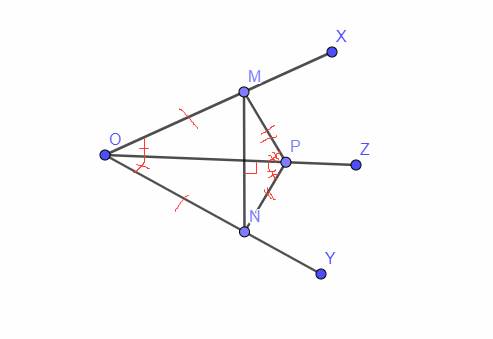
Cho Oz la tia phân giác cua goc xOy nhon. Trên các tia Ox,Oy lần lượt lấy 2 điểm M,N sao cho OM=ON.Gọi R là giao điểm MN va Oz , K la điểm bất kì trên tia Oz .
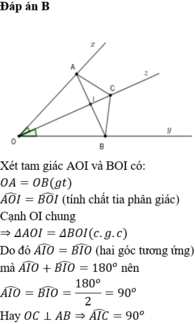
a, so sánh tam giác OMK và tam giác ONK
b, cmr OKvuông góc với MN
c, Gọi giao điểm MK và Oy là E.CMR:tia phân giác của góc NKE//MN