Cho tam giác MNP, H là hình chiếu của M trên NP, chứng minh 2MH + NP lớn hơn MN + MP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
8 tháng 11 2023
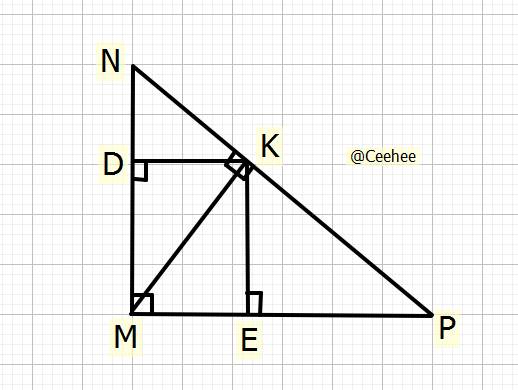
`a)` Biết `MN=7cm;NP=25cm`
Xét \(\Delta MNP\) vuông tại `M`, đường cao `MK`
Ta có: \(NP^2=MN^2+MP^2\) (đl Pytago)
\(\Rightarrow25^2=7^2+MP^2\\ \Rightarrow MP^2=25^2-7^2=576\\ \Rightarrow MP=\sqrt{576}=24cm\)
Ta có: \(\dfrac{1}{MK^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{MK^2}=\dfrac{1}{7^2}+\dfrac{1}{24^2}\\ \Rightarrow\dfrac{1}{MK^2}=\dfrac{625}{28224}\\ \Rightarrow MK^2=\dfrac{1\cdot28224}{625}\\ \Rightarrow MK=\sqrt{\dfrac{28224}{625}}\\ \Rightarrow MK=6,72cm\)
Ta có: \(MN^2=NK\cdot NP\left(htl\right)\)
\(\Rightarrow7^2=NK\cdot25\\ \Rightarrow NK=\dfrac{7^2}{25}=1,96cm\)
Vậy: \(MP=24cm;MK=6,72cm;NK=1,96cm\)
`b)` \(C/m:MD\cdot MN=ME\cdot MP\)
Xét \(\Delta KMN\) vuông tại `K`
Ta có: \(MK^2=MD\cdot MN\left(htl\right)\left(1\right)\)
Xét \(\Delta KMP\) vuông tại `K`
Ta có: \(MK^2=ME\cdot MP\left(htl\right)\left(2\right)\)
Từ `(1)` và `(2)` \(\Rightarrow MK^2=MK^2\)
\(\Rightarrow MD\cdot MN=ME\cdot MP\left(=MK^2\right)\)
(Câu `c)` tớ chịu :v).
28 tháng 8 2021
2: Áp dụng hệ thức lượng trong tam giác vuông vào ΔMHN vuông tại H có HD là đường cao ứng với cạnh huyền MN, ta được:
\(MD\cdot MN=MH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔMHP vuông tại H có HE là đường cao ứng với cạnh huyền MP, ta được:
\(ME\cdot MP=MH^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MN=ME\cdot MP\)
20 tháng 6 2023
a: Xét ΔHNM vuông tại H và ΔMNP vuôg tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
c; Đề bài yêu cầu gì?
UT
18 tháng 4 2021
tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)
28 tháng 8 2023
a: ΔPIM vuông tại I
=>IP^2+IM^2=MP^2
=>IM^2=10^2-6^2=64
=>IM=8(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên PI*PN=PM^2
=>PN=10^2/6=50/3(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên MI^2=IN*IP
=>IN=8^2/6=32/3(cm)
Xét ΔMNP vuông tại M có sin MNP=MP/PN
=10:50/3=3/5
=>góc MNP=37 độ
b: C=MN+NP+MP
=10+40/3+50/3
=10+90/3
=10+30
=40(cm)
c: Xét ΔIMP vuông tại I có IK là đường cao
nên IK*PM=IP*IM
=>IK*10=6*8=48
=>IK=4,8(cm)
