Bài 1 :Hình trụ có chiều cao gấp 3 lần đường kính đáy. Biết thể tích V=162 pi cm^3. Tính Stp của hình trụ.
Bài 2 : - Cho A nằm ngoài (O, R). Kẻ tiếp tuyến AB, AC. H là giao của OA và BC, kẻ dây MN qua H với M thuộc cung nhỏ BC và BM < CM
chứng minh HM.HN= HB.HC và chứng minh góc CAN=MAB
làm hộ mk bài này vs. cảm ơn rất...
Đọc tiếp
Bài 1 :Hình trụ có chiều cao gấp 3 lần đường kính đáy. Biết thể tích V=162 pi cm^3. Tính Stp của hình trụ.
Bài 2 : - Cho A nằm ngoài (O, R). Kẻ tiếp tuyến AB, AC. H là giao của OA và BC, kẻ dây MN qua H với M thuộc cung nhỏ BC và BM < CM
chứng minh HM.HN= HB.HC và chứng minh góc CAN=MAB
làm hộ mk bài này vs. cảm ơn rất nhiều
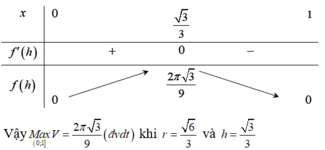
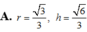
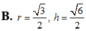
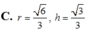
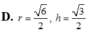
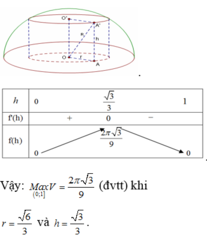
Làm nốt bài 2 nhé. Hôm qua mình bận nên không làm tiếp được
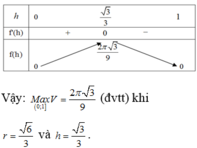
Bài 2:
a) 4 điểm $C,M,B,N$ cùng thuộc $(O)$ nên $CNBM$ là tứ giác nội tiếp.
$\Rightarrow HC.HB=HM.HN$ (đây là tính chất quen thuộc)
Nếu muốn chứng minh chi tiết bạn có thể chỉ ra $\triangle HMB\sim \triangle HCN$ (g.g)
$\Rightarrow \frac{HM}{HC}=\frac{HB}{HN}\Rightarrow HM.HN=HB.HC$
b)
Vì $AC=AB$ (tính chất 2 tiếp tuyến cắt nhau tại 1 điểm). $OB=OC=R$ nên $OA$ là trung trực của $BC$
$\Rightarrow OA\perp BC$ tại $H$ và $H$ là trung điểm của $BC$. Từ đây ta có:
Tam giác $ACO$ vuông tại $C$, có $CH\perp AO$, áp dụng công thức hệ thức lượng trong tam giác vuông thì:
$HA.HO=CH^2$.
Mà $CH=BH$ (do $H$ là trung điểm của $BC$) nên $HA.HO=HC.HB$
Kết hợp với kết quả phần a suy ra $HA.HO=HM.HN$
$\Rightarrow \triangle AMON$ nội tiếp
$\Rightarrow \widehat{NAO}=\widehat{NMO}$ và $\widehat{MAO}=\widehat{MNO}$
Mà $\widehat{NMO}=\widehat{MNO}$ (do tam giác $MON$ cân tại $O$)
$\Rightarrow \widehat{NAO}=\widehat{MAO}(1)$
Mặt khác, cũng theo tính chất 2 tiếp tuyến cắt nhau tại 1 điểm, $AO$ là phân giác $\widehat{CAB}$ nên $\widehat{CAO}=\widehat{BAO}(2)$
Lấy $(2)-(1)$ suy ra $\widehat{CAN}=\widehat{MAB}$ (đpcm)
cảm ơn bạn