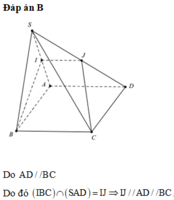
cho hình bình hành ABCD có S=27 cm2.M là trung điểm của DC.Tính S ABMD?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 9 2019
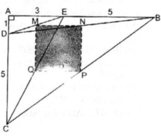
△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S
S
20 tháng 7 2023
a) Để so sánh diện tích hai tam giác ABC và ADC, ta cần biết độ dài hai cạnh AB và CD. Tuy nhiên, trong đề bài không cho biết giá trị cụ thể của AB và CD, chỉ biết rằng AB = 1/3 CD. Do đó, không thể xác định được quan hệ so sánh diện tích hai tam giác này.
b) Ta có AM = MB và CM = MC (do M là điểm chung của đường chéo AC). Vì vậy, diện tích hai tam giác ABM và ACM sẽ bằng nhau.
c) Diện tích hình thang ABCD bằng 64 cm^2. Để tính diện tích tam giác MBA, ta cần biết chiều cao từ đỉnh M xuống đáy AB. Tuy nhiên, trong đề bài không cung cấp thông tin về chiều cao này, do đó không thể tính được diện tích tam giác MBA.
A
23 tháng 1 2021
a) Kẻ BH vuông góc với AD.
SABCD=BH.AD=BH.2BM=S
=> BH.BM=
Có AD song song với BM (ABCD là hbh)
SABMD=
b) Nối A với M. T là trung điểm của AD. Nối B với T.
Ta có: TDMB là hbh (TD song song với BM; TD=BM=)
=> TF là đường TB của tam giác ADN => AF=FN (1)
MN là đường TB của tam giác BCF => FN=NC (2)
Từ (1)(2)=> AF=FN=NC
Ta có: SNMC=SFMN=SAFM
mà SABC = và SABM=SACM => SAMC=
=> SMNC =
=> SABMN = SABC-SMNC =
13 tháng 8 2023
a: Xét tứ giác MCDN có
MC//DN
MC=DN
MC=CD
=>MCDN là hình thoi
b: Xét ΔCMD có CM=CD và góc C=60 độ(=góc BAD)
nên ΔCMD đều
=>góc CMD=60 độ
góc BMD+góc CMD=180 độ(kề bù)
=>góc BMD=180-60=120 độ
=>góc BMD=góc B
Xét tứ giác ABMD có
BM//AD
góc ABM=góc BMD
=>ABMD là hình thang cân
=>AM=BD
c: Xét ΔKAD có BM//AD
nên BM/AD=KM/KD=KB/KA
=>KM/KD=KB/KA=1/2
=>Mlà trung điểm của KD, B là trung điểm của KA
Xét ΔKAD có
AM,DB,KN là trung tuyến
=>AM,DB,KN đồng quy
CM
4 tháng 3 2019
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME ^ BD tại E, CF ^ BD tại F.
Có B N = 1 3 B D , E M = 1 2 C F S B M N = 1 2 E M . B N = 1 2 . 1 2 C F . 1 3 B D = 1 6 S B C D = 1 12 S ⇒ S M N D C = 1 2 S − 1 12 S = 5 12 S
19 tháng 3 2017
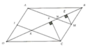
a) Kẻ BH vuông góc với AD.
SABCD=BH.AD=BH.2BM=S
=> BH.BM=\(\dfrac{S}{2}\)
Có AD song song với BM (ABCD là hbh)
SABMD=\(\dfrac{\left(AD+BM\right).BH}{2}=\dfrac{3BM.BH}{2}=\dfrac{3}{2}.\dfrac{S}{2}=\dfrac{3S}{4}\)
b) Nối A với M. T là trung điểm của AD. Nối B với T.
Ta có: TDMB là hbh (TD song song với BM; TD=BM=\(\dfrac{1}{2}BC\))
=> TF là đường TB của tam giác ADN => AF=FN (1)
MN là đường TB của tam giác BCF => FN=NC (2)
Từ (1)(2)=> AF=FN=NC
Ta có: SNMC=SFMN=SAFM
mà SABC =\(\dfrac{S}{2}\) và SABM=SACM => SAMC= \(\dfrac{S}{4}\)
=> SMNC = \(\dfrac{S}{4}:3=\dfrac{S}{12}\)
=> SABMN = SABC-SMNC = \(\dfrac{S}{2}-\dfrac{S}{12}=\dfrac{5S}{12}\)
GV
Giáo viên Toán
Giáo viên
29 tháng 4 2017
a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S
