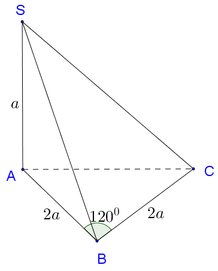
Cho hình chóp S.ABC có SA=2a, SA ⊥ (ABC), tam giác ABC vuông tại B và AB=a. Khoảng cách từ điểm A đến mặt phẳng (SBC) là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
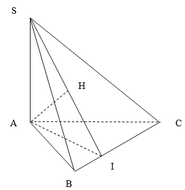
Gọi I, H lần lượt là hình chiếu của A lên BC và SI
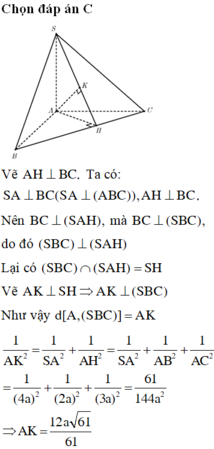
Ta có: 1 A I 2 = 1 A B 2 + 1 A C 2 = 1 2 a 2 + 1 3 a 2 = 13 36 a 2
1 A H 2 = 1 S A 2 + 1 A I 2 = 1 4 a 2 + 1 36 a 2 = 61 144 a 2
⇒ A I = 12 a 61 ⇒ d = A I = 12 a 61
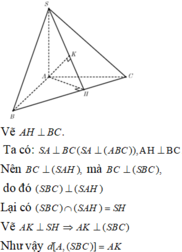


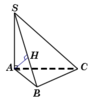
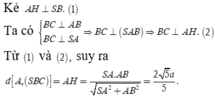


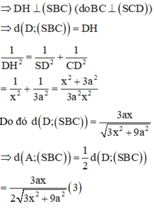


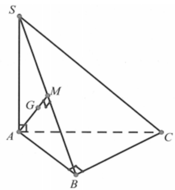
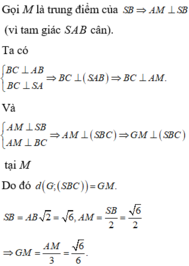
Kẻ đường cao AH của \(\Delta SAB\)
Ta có: SA\(\perp\)( ABC ) = > SA\(\perp\)BC
mà AB \(\perp\)BC ( tam giác ABC vuông tại B )
=> BC \(\perp\)(SAB ) => BC \(\perp\)AH lại có: AH \(\perp\)SB ( theo cách vẽ đường cao)
=> AH \(\perp\)(SBC )
=> d ( A; (SBC )) = AH
Xét \(\Delta\)SAB vuông tại A có AH là đường cao
=> \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{SA^2}=\frac{1}{a^2}+\frac{1}{4a^2}=\frac{5}{4a^2}\Rightarrow AH=\frac{2\sqrt{5}}{5}\)
Vậy d ( A; (SBC )) = AH = \(\frac{2\sqrt{5}}{5}\)