Giải t3-6(m-1)t2+(11m2-18m+6)t-6m3+13m2-6m=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 11 2019
s = 6 t 2 − t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V C Đ = v(2) = 12(m/s).
CM
14 tháng 12 2018
s = 6 t 2 – t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V CD = v(2) = 12(m/s).
VT
25 tháng 2 2017
Đáp án A
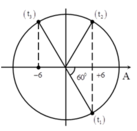
Ta thấy tại thời điểm t1 và t2 có x1 = x2 nên nó đối xứng nhau qua trục Ox.
+ Tới thời điểm t3 thì x3 = - x1 nên thời gian đi từ x1 đến x3 là T 2
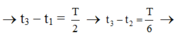
Góc lệch giữa vị trí x2 và x3 là:
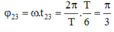
® Góc lệch giữa x1 và x2 là:
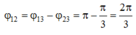
Vậy góc lệch của x1 so với vị trí vật đạt cực đại của dao động là
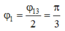
Mà x1 = A.cosj1 = 6 ® A = 12 cm
16 tháng 10 2023
Ta có:
5/6+7,7+5,9=[Số t1+ Số t2+ Số t3]*2
14,43333333=[số t1+số t2+số t3]
Suy ra:Số t1+ số t2+ số t3=14,43333333:2
Số t1+số t2+số t3=7,216666667
Đến đây dễ rồi, tự làm tiếp
TM
1
21 tháng 3 2022
\(\Leftrightarrow6t^2-12-5t-38=0\)
\(\Leftrightarrow6t^2-5t-50=0\)
\(\Leftrightarrow\left(3t-10\right)\left(2t+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{10}{3}\\t=-\dfrac{5}{2}\end{matrix}\right.\)