Cho tam giác ABC có AB=2,BC=3,CA=4cm đồng dạng với tam giác MNP.Tính độ dài các cạnh của tam giác MNP biết chu vi MNP là 36
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2019
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
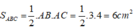
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
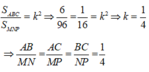
Thay số
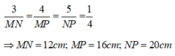
Chọn đáp án B
8 tháng 1
ΔABC đồng dạng với ΔMNP
=>\(\dfrac{AB}{MN}=\dfrac{BC}{NP}=\dfrac{AC}{MP}\)
ΔABC đồng dạng với ΔMNP
=>Độ dài cạnh nhỏ nhất của ΔMNP sẽ là độ dài tương ứng với cạnh nhỏ nhất của ΔABC
mà cạnh nhỏ nhất của ΔABC là AB và cạnh tương ứng của AB trong ΔMNP là MN
nên MN=2,5cm
=>\(\dfrac{5}{2,5}=\dfrac{12}{MP}=\dfrac{13}{NP}\)
=>\(\dfrac{12}{MP}=\dfrac{13}{NP}=2\)
=>MP=12/2=6(cm); NP=13/2=6,5(cm)
CM
18 tháng 10 2019
Vì tam giác ABC đồng dạng với tam giác MNP nên;
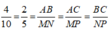
Theo tính chất dãy tỉ số bằng nhau ta có:
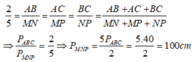
Chọn đáp án C
3 tháng 12 2023
ΔDEF đồng dạng với ΔMNP
=>\(\dfrac{DE}{MN}=\dfrac{EF}{NP}=\dfrac{DF}{MP}\)
=>\(\dfrac{MN}{DE}=\dfrac{NP}{EF}=\dfrac{MP}{DF}\)
=>\(\dfrac{MN}{4}=\dfrac{NP}{7}=\dfrac{MP}{8}\)
Chu vi tam giác MNP bằng 38cm nên MN+NP+MP=38
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MN}{4}=\dfrac{NP}{7}=\dfrac{MP}{8}=\dfrac{MN+NP+MP}{4+7+8}=\dfrac{38}{19}=2\)
=>\(MN=4\cdot2=8\left(cm\right);NP=7\cdot2=14\left(cm\right);MP=8\cdot2=16\left(cm\right)\)
17 tháng 5 2021
Ta có tam giác ABC = tam giác MNP
=> AB = MN = 5 cm
=> AC = MP = 8 cm
Lại có : \(P_{MNP}=MN+NP+MP=20\)
\(\Rightarrow5+8+NP=20\Leftrightarrow NP=7\)cm
Vậy AB = 5 cm ; NP = 7 cm ; MP = 8 cm
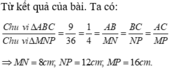
AB/MN=BC/NP=CA/PM=(AB+BC+CA)/(MN+NP+PM)=(2+3+4)/36=1/4
=> AB/MN=2/MN=1/4=> MN=8
Tương tự tính ra NP và PM
Tính chu vi của tam giác ABC là:9cm
Lấy chu vi tam giác MNP/tam giác ABC là: 36/9=4cm
=>MN=4.2=8(cm)
NP=4.3=12(cm)
MP=4.4=16(cm)