x^3-7x^2+15x-25=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 9 2017
\(x^3-7x^2+15x-25=0\)
\(\Leftrightarrow\left(x^3-5x^2\right)-\left(2x^2-10x\right)+\left(5x-25\right)=0\)
\(\Leftrightarrow x^2\left(x-5\right)-2x\left(x-5\right)+5\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2-2x+5\right)=0\)(*)
Ta thấy \(x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4>0\forall x\)
Dể pt (*) xảy ra \(\Leftrightarrow x-5=0\Leftrightarrow x=5\)
Vậy \(x=5\)
HT
14 tháng 9 2017
x^3 - 7x^2 + 15x - 25 = 0
x3 + -7x2 + 15x + -25 = 0
Sắp xếp lại các điều khoản: -25 + 15x + -7x2 + x3 = 0
Giải quyết -25 + 15x + -7x2 + x3 = 0
Giải quyết cho biến 'x'.
P/s : Giải pháp cho phương trình này không thể xác định.
Mk nghĩ là vậy , chúc bạn thành công trong cuộc sống !
13 tháng 4 2020
Ta có: \(x^3-7x^2+15x-25=0\)
\(\Leftrightarrow\left(x^3-5x^2\right)-\left(2x^2-10x\right)+\left(5x-25\right)=0\)
\(\Leftrightarrow x^2\left(x-5\right)-2x\left(x-5\right)+5\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2-2x+5\right)=0\)(1)
Ta có: \(x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\)
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^2+4\ge4>0\forall x\)
hay \(x^2-2x+5>0\forall x\)(2)
Từ (1) và (2) suy ra x-5=0
hay x=5
Vậy: x=5
19 tháng 1 2016
\(x^3-5x^2-2x^2+10x+5x-25=0\)
<=>\(x^2.\left(x-5\right)-2x\left(x-5\right)+5.\left(x-5\right)=\left(x-5\right)\left(x^2-2x+5\right)=0\)
<=>hoặc x-5=0 =>x=5
hoặc x^2-2x+5=0 (tự biến đổi ra ) <=>(x-1)^2=-4(loại)
Vậy nghiệm của pt là x=5
19 tháng 1 2016
<=>\(x^3-7x^2+15x-25=\left(x-5\right)\left(x^2-2x+5\right)\)
=>\(x^2-2x+5=0\)
có biệt thức
\(\left(-2\right)^2-4\left(1.5\right)=-16\)
=>PT trên ko có nghiệm
=>x=5
24 tháng 10 2021
c: ta có: \(7x^2-2x-5=0\)
\(\Leftrightarrow\left(x-1\right)\left(7x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{5}{7}\end{matrix}\right.\)
10 tháng 4 2020
\(b, (2x^2 + 3x-1) - 5(2x^2 + 3x + 2) + 24 =0 \)
Đặt \(2x^2 + 3x + 1 = a \)
\(=> (a-2) - 5(a+2) + 24 = 0\)\(\)
\(=> a - 2 - 5a - 10 + 24 = 0\)
\(=> a = 3=> 2x^2 + 3x + 1 = 3\)
\(<=> 2x^2 + 3x - 2 = 0\)
\(<=> 2x^2 + 4x - x - 2 = 0\)
\(<=> (2x-1)(x+2) = 0 \)
\(<=> 2x - 1 = 0 hoặc x+2 =0\)
\(<=> x = 1/2 hoặc x = -2\)
~~
LV
1
24 tháng 10 2021
c: ta có: \(7x^2-2x-5=0\)
\(\Leftrightarrow\left(x-1\right)\left(7x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{5}{7}\end{matrix}\right.\)
29 tháng 12 2021
c: \(=\dfrac{\left(x-5\right)\left(x+5\right)}{3x+4}\cdot\dfrac{-5}{x-5}=\dfrac{-5\left(x+5\right)}{3x+4}\)
31 tháng 7 2021
a) Ta có: \(7x\left(x-20\right)-x+20=0\)
\(\Leftrightarrow\left(x-20\right)\left(7x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=\dfrac{1}{7}\end{matrix}\right.\)
b) Ta có: \(x^3-15x=0\)
\(\Leftrightarrow x\left(x-\sqrt{15}\right)\left(x+\sqrt{15}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{15}\\x=-\sqrt{15}\end{matrix}\right.\)
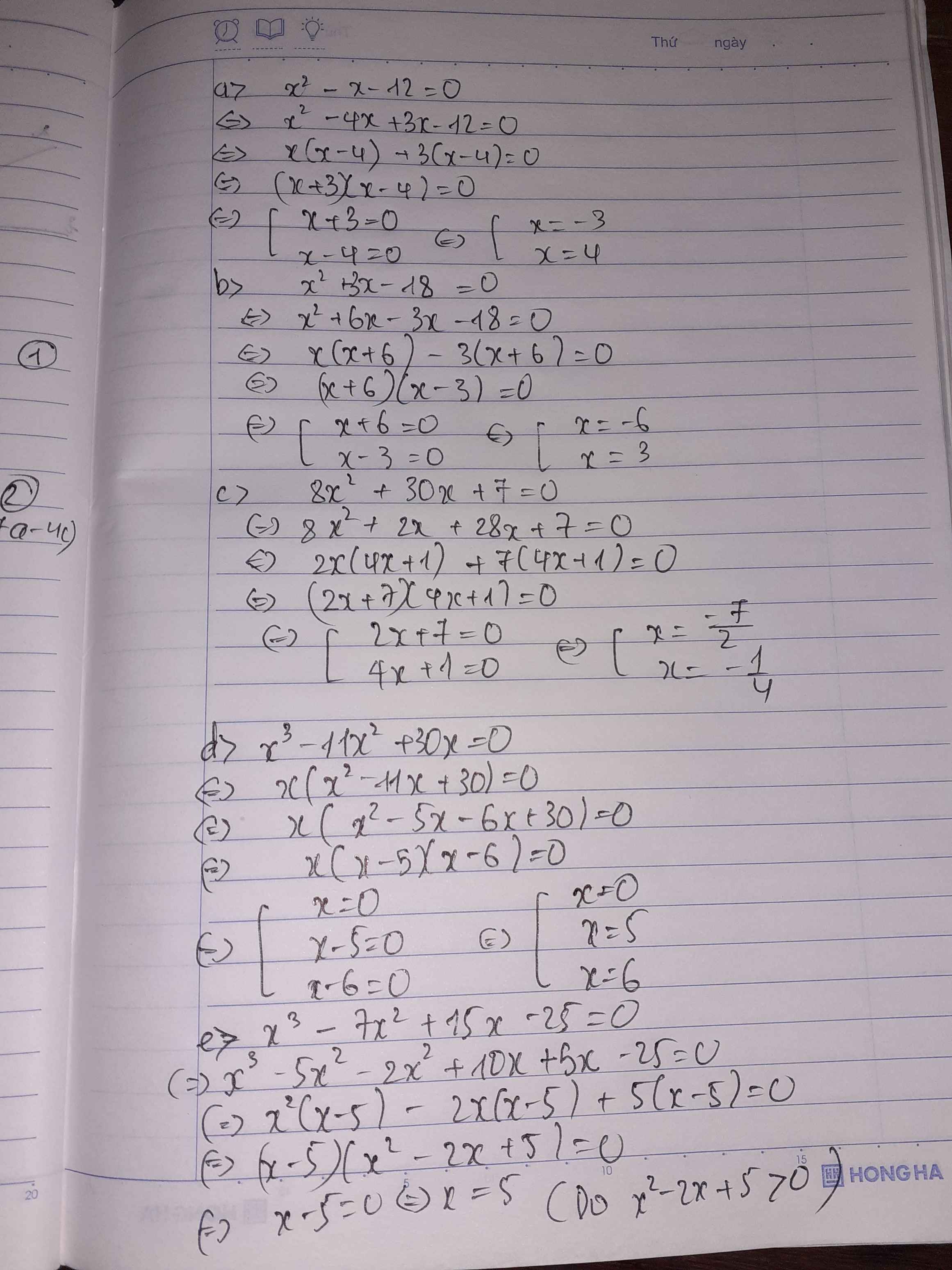
\(x^3-7x^2+15x-25=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2-2x+5\right)=0\)
zì \(x^2-2x+5=\left(x-1\right)^2+4>0\left(\forall x\right)nên,x-5=0\)
=> x=5