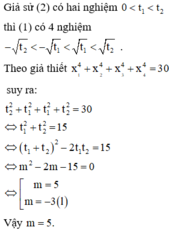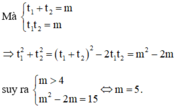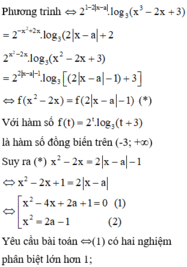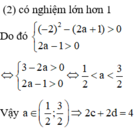Cho phương trình x4+2mx2+4=0 . Tìm giá trị của tham số m để phương trình có
4 nghiệm phân biệt x1,x2,x3,x4 thoả mãn x14+x24+x34+x44=32
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 2 2018
Đáp án A
Phương trình hoành độ giao điểm của (C) và Ox là x 4 − m x 2 + m = 0 * .
Đặt t = x 2 ≥ 0 khi đó * ⇔ f t = t 2 − m t + m = 0
Để (*) có 4 nghiệm phân biệt ⇔ f t = 0 có 2 nghiệm dương phân biệt t 1 , t 2
Khi đó, gọi t 1 , t 2 t 1 < t 2 là hai nghiệm phân biệt của f t = 0
Suy ra:
x 1 = − t 2 ; x 2 = − t 1 ; x 3 = t 1 ; x 4 = t 2 ⇒ x 1 4 + x 2 4 + x 3 4 + x 4 4 = 2 t 1 2 + t 2 2 = 30
Mà t 1 + t 2 = m t 1 t 2 = m
⇒ t 1 2 + t 2 2 = t 1 + t 2 2 − 2 t 1 t 2 = m 2 − 2 m
suy ra m > 4 m 2 − 2 m = 15 ⇔ m = 5.
4 tháng 6 2021
Để pt có nghiệm \(\Leftrightarrow\Delta\ge0\Leftrightarrow4-4\left(m-1\right)\ge0\)\(\Leftrightarrow2\ge m\)
Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^4-x_1^3=x_2^4-x_2^3\)
\(\Leftrightarrow\left(x_1^4-x_2^4\right)-\left(x_1^3-x_2^3\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)\left(x_1^2+x_2^2\right)-\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left[2\left(x_1^2+x_2^2\right)-x_1^2-x_1x_2-x_2^2\right]=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1^2+x_2^2-x_1x_2\right)=0\)
\(\Leftrightarrow x_1-x_2=0\) (2) ( vì \(x_1^2-x_1x_2+x_2^2>0;\forall x,y\))
Từ (1) (2) \(\Rightarrow x_1=x_2=1\)
\(\Rightarrow x_1x_2=m-1=1\) \(\Leftrightarrow m=2\) (Thỏa)
Vậy...
CM
17 tháng 9 2018
b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
CM
4 tháng 5 2018
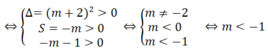
Đáp án A
Ghi nhớ: Nếu hàm số 
liên tục trên đoạn 
và 
thì phương trình 
có ít nhất một nghiệm nằm trong khoảng 
.