tìm tập nghiệm của phương trình \(2^{x^4}=16\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
14 tháng 12 2017
Phương trình tương đương với:
2 x 2 - x + 4 = 16 ⇔ x 2 - x + 4 = 4 ⇔ x 2 - x = 0 ⇔ x = 0 ; x = 1 .
Chọn đáp án A.
5 tháng 6 2021
\(x^2-\left(m+4\right)x+4m=0\) (1)
a)Thay x=2 vào pt (1) ta được: \(4-\left(m+4\right).2+4m=0\) \(\Leftrightarrow m=2\)
Thay m=2 vào pt (1) ta được: \(x^2-6x+8=0\)\(\Leftrightarrow x^2-4x-2x+8=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-2\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
Vậy nghiệm còn lại là 4
b)Để pt có hai nghiệm pb \(\Leftrightarrow\Delta>0\Leftrightarrow m^2-8m+16>0\)\(\Leftrightarrow\left(m-4\right)^2>0\)\(\Leftrightarrow m\ne4\)
Do x1 là một nghiệm của pt \(\Rightarrow x_1^2-\left(m+4\right)x_1+4m=0\)
\(\Rightarrow x_1^2=\left(m+4\right)x_1-4m=0\)
Theo viet có: \(x_1+x_2=m+4\)
\(x_1^2+\left(m+4\right)x_2=16\)
\(\Leftrightarrow\left(m+4\right)x_1-4m+\left(m+4\right)x_2=16\)
\(\Leftrightarrow\left(m+4\right)\left(x_1+x_2\right)-4m-16=0\)
\(\Leftrightarrow\left(m+4\right)^2-4m-16=0\)
\(\Leftrightarrow m^2+4m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-4\end{matrix}\right.\)(Thỏa)
Vậy...
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
DN
3
28 tháng 2 2022
\(\Leftrightarrow x^2+5x+6-x^2+4x=0\)
=>9x+6=0
hay x=-2/3
DN
2
28 tháng 2 2022
\(\Leftrightarrow x-1-5x-4+5x^2-10x=0\)
\(\Leftrightarrow5x^2-14x-5=0\)
\(\text{Δ}=\left(-14\right)^2-4\cdot5\cdot\left(-5\right)=296>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{14-2\sqrt{74}}{10}=\dfrac{7-\sqrt{74}}{5}\\x_2=\dfrac{7+\sqrt{74}}{5}\end{matrix}\right.\)
28 tháng 2 2022
\(\left(x-1\right)-\left(5x+4\right)+5x\left(x-2\right)=0\\ \Leftrightarrow x-1-5x-4+5x^2-10x=0\\ \Leftrightarrow5x^2-14x-5=0\)
\(\Delta=\left(-14\right)^2-4.5.\left(-5\right)=196+100=296\)
\(x_1=\dfrac{-\left(-14\right)+\sqrt{296}}{2.5}=\dfrac{14+2\sqrt{74}}{10}=\dfrac{7+\sqrt{74}}{5}\)
\(x_2=\dfrac{-\left(-14\right)-\sqrt{296}}{2.5}=\dfrac{14-2\sqrt{74}}{10}=\dfrac{7-\sqrt{74}}{5}\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Ta có: \({x^2} + x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
\( \Rightarrow A = \{ 1; - 2\} \)
Ta có: \(2{x^2} + x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2}\\x = - 2\end{array} \right.\)
\( \Rightarrow B = \left\{ {\frac{3}{2}; - 2} \right\}\)
Vậy \(C = A \cap B = \{ - 2\} \).
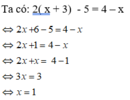
\(2^{x^4}=16\)
<=> 24x = 16
<=> 24x = 24
<=> 4x = 4
<=> x = 1
\(2^{x^4}=16\)
\(\Leftrightarrow x^4=4\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)