Cho tam giác ABC có M là trung điểm BC.Bt ^BAM=^CAM.Cm ABC cân tại A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


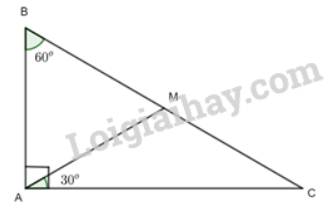
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.

Tam giác ABC có :
BM=CM(GT)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
Một tam giác có tia phân giác đồng thời là đường trung tuyến thì là tam giác cân
=> Tam giác ABC cân tại A (đccm)
Ok cách khác
Kẻ \(MD\perp AB;ME\perp AC\)
Xét tam giác ADM và AEM, có :
\(\widehat{ADM}=\widehat{AEM}=90^o\)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
AM-cạnh chung
=> Tam giác ADM=AEM(cạnh huyền-góc nhọn)
=> DM=ME
Xét tam giác BMD và CME,có :
DM=ME(cmt)
\(\widehat{MEC}=\widehat{MDB}=90^o\)
BM=CM(gt)
=> Tam giác BMD=CME(cạnh huyền-cạnh góc vuông)
=> \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A (2 góc đáy bằng nhau)
*Hơi dài dòng TÍ

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường cao
nên AM là tia phân giác của góc BAC
hay góc BAM= góc CAM
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
hay ΔMHK cân tại M
d: Xét ΔAHK có AH=AK
nên ΔAHK cân tại A
e: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
Vì M là trung điểm của BC nên suy ra AM là trung tuyến và \(\widehat{BAM}=\widehat{CAM}\)suy raAM là trung tuyến
Xét \(\Delta ABC\)có AM là trung tuyến đồng là tia phân giác \(\Rightarrow\Delta ABC\)cân tại A
Hok tốt
Hình chắc bác cx tự vẽ đc
+) Kẻ \(\hept{\begin{cases}HM\perp AB\\MK\perp AC\end{cases}}\) ( tại H và tại K )
Xét \(\Delta\) AHM vuông tại H và \(\Delta\) AKM vuông tại K có
AM : cạnh chung
\(\widehat{BAM}=\widehat{CAM}\) ( gt)
=> \(\Delta\)AHM = \(\Delta\) AKM ( ch-gn)
=> HM = KM ( 2 cạnh tương ứng )
+) Xét \(\Delta\)BHM vuông tại H và \(\Delta\) CKM vuông tại K có
BM = MC ( gt)
HM = KM ( cmt)
=> \(\Delta\) BHM = \(\Delta\) CKM ( ch -cgv)
=> \(\widehat{B}=\widehat{C}\) ( 2 cạnh tương ứng )
+) Xét \(\Delta\)ABC có
\(\widehat{B}=\widehat{C}\)
=> \(\Delta\) ABC cân tại A
@@ Học tốt
Chiyuki Fujito