Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\left\{{}\begin{matrix}AB=AC\\\widehat{BAM}=\widehat{CAM}\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta BAM=\Delta CAM\left(c.g.c\right)\\ b,\Delta BAM=\Delta CAM\\ \Rightarrow MB=MC\\ \Rightarrow M\text{ là trung điểm }BC\\ c,\Delta BAM=\Delta CAM\\ \Rightarrow\widehat{AMB}=\widehat{AMC}\\ \text{Mà }\widehat{AMB}+\widehat{AMC}=180^0\\ \Rightarrow\widehat{AMB}=90^0\\ \Rightarrow AM\bot BC\)

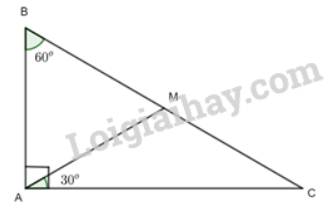
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
Tam giác ABC có :
BM=CM(GT)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
Một tam giác có tia phân giác đồng thời là đường trung tuyến thì là tam giác cân
=> Tam giác ABC cân tại A (đccm)
Ok cách khác
Kẻ \(MD\perp AB;ME\perp AC\)
Xét tam giác ADM và AEM, có :
\(\widehat{ADM}=\widehat{AEM}=90^o\)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
AM-cạnh chung
=> Tam giác ADM=AEM(cạnh huyền-góc nhọn)
=> DM=ME
Xét tam giác BMD và CME,có :
DM=ME(cmt)
\(\widehat{MEC}=\widehat{MDB}=90^o\)
BM=CM(gt)
=> Tam giác BMD=CME(cạnh huyền-cạnh góc vuông)
=> \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A (2 góc đáy bằng nhau)
*Hơi dài dòng TÍ