Cho hình thang ABCD (AB//CD) có BD2=AB.CD. Chứng minh đường tròn
ngoại tiếp tam giác ABD tiếp xúc với BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
16 tháng 11 2017
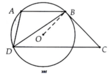
Chứng minh được: ∆DBC:∆BAD => D B C ^ = B A D ^
=> s đ D B C ⏜ = 1 2 s đ B m D ⏜
=> BC là tiếp tuyến của (O)

CM
28 tháng 3 2019
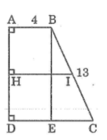
Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
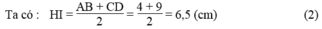
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD