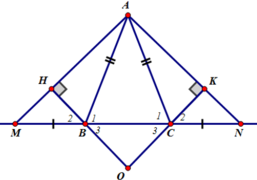
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB.
a) Chứng minh tam giác AMN là tam giác đều;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2016
chăng co tam giac vuong can nao ma bm=cn = ab lan sau hoi bai thi hoi dang hoang
keo lam kho nguoi khac
3 tháng 2 2016
a) Xét tam giác ABM và tam giác ACN có
AB =AC (gt)
B^=C^ (gt)
BM=CN (gt)
=> tam giác ABM = tam giác ACN (c-g-c)
=> AN=AM ( cctư)
Xét tam giác AMN có
AM=AN ( cmt)
=> tam giác AMN cân tại A
Bn tham khảo nhé!
CM
16 tháng 2 2017
ΔABC cân tại A suy ra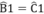 
Ta lại có :
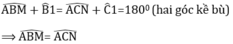
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
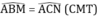
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.
HL
27 tháng 2 2015
Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)
Ta có : tam giác ABC cân tại A (gt) (2)
Từ(1) và(2)=> HB=HC(=1/2 BC) (3)
Lại có: BM=CN (gt) (4)
M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)
Từ (3)và (4)=>HB+BM=HC+CN (6)
Từ (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN
=> Tam giác AMN cân tại A (đpcm)