Tìm m sao cho với mọi x, ta có: 2x3−3x2+x+m2x3−3x2+x+m=(x+2)(2x2−7x+15)
Ai còn on ko kb đi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 1 2022
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^4-10x^3+6x^2\)
c: \(=-x^5+2x^3-\dfrac{3}{2}x^2\)
d: \(=2x^3+10x^2-8x-x^2-5x+4=2x^3+9x^2-13x+4\)
CM
8 tháng 5 2019
Ta có
M ( x ) = P ( x ) − Q ( x ) = − 6 x 5 − 4 x 4 + 3 x 2 − 2 x − 2 x 5 − 4 x 4 − 2 x 3 + 2 x 2 − x − 3 = − 8 x 5 + 2 x 3 + x 2 − x + 3 Có M ( − 1 ) = − 8. ( − 1 ) 5 + 2 ⋅ ( − 1 ) 3 + ( − 1 ) 2 − ( − 1 ) + 3 = 11
Chọn đáp án A
C
12 tháng 4 2022
a) f (x) = 3x2 + 5x3 - 7x - 9
Hệ số cao nhất là: 5
Hệ số tự do là: 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
g(x) = ( 8x2 - 3x2) + ( 8-5) + ( -2x3 + 2x3) -9x
g(x) = 5x2 + 3 -9x
Hệ số cao nhất là: 5
Hệ số tự do là: 3
12 tháng 4 2022
a) f (x) = 3x2 + 5x3 - 7x - 9
Hệ số cao nhất là: 5
Hệ số tự do là: 9
b) g(x) = 8x2 + 8 - 2x3 - 3x2 - 9x + 2x3 - 5
g(x) = ( 8x2 - 3x2) + ( 8-5) + ( -2x3 + 2x3) -9x
g(x) = 5x2 + 3 -9x
Hệ số cao nhất là: 5
Hệ số tự do là: 3
2
18 tháng 4 2022
`a) A(x) + M(x) = B(x)`
`->( 2x^2 - 5 + 9x ) + M(x) = ( 3x^2 + 9x - 1 )`
`-> M(x) = ( 3x^2 + 9x - 1 ) - ( 2x^2 - 5 + 9x )`
`-> M(x) = 3x^2 + 9x - 1 - 2x^2 + 5 - 9x`
`-> M(x) = x^2 + 4`
__________________________________
`b)` Cho `M(x) = 0`
`-> x^2 + 4 = 0`
`-> x^2 = -4` (Vô lí vì `x^2 >= 0` mà `-4 < 0`)
Vậy đa thức `M(x)` không có nghiệm
18 tháng 4 2022
a, ta có A(x) + M(x)= B(x)
=> M(x)= B(x) - A(x)= (3x2+9x-1) -(2x2-5+9x)
= 3x2+9x-1 -2x2 +5 -9x
= (3x2-2x2) +( 9x-9x)+(5-1)
= x2 +4
b, Ta có x2> hoặc bằng 0 => x2+4 >0
24 tháng 6 2021
a)\(f\left(x\right)=2x^2-x-3+5=\left(x+1\right)\left(2x-3\right)+5\)
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(x+1\right)\left(2x-3\right)+5⋮\left(x+1\right)\)
\(\Leftrightarrow5⋮\left(x+1\right)\)
mà \(x+1\in Z\Rightarrow x+1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{-2;0;4;-6\right\}\)
Vậy...
b) \(f\left(x\right)=3x^2-4x+6=\left(3x^2-4x+1\right)+5=\left(3x-1\right)\left(x-1\right)+5\)
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(3x-1\right)\left(x-1\right)+5⋮\left(3x-1\right)\)
\(\Leftrightarrow5⋮\left(3x-1\right)\) mà \(3x-1\in Z\Rightarrow3x-1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{0;\dfrac{2}{3};2;-\dfrac{4}{3}\right\}\) mà x nguyên\(\Rightarrow x\in\left\{0;2\right\}\)
Vậy...
c)\(f\left(x\right)=\left(-2x^3-7x^2-5x+2\right)+3\)\(=\left(-2x^3-4x^2-3x^2-6x+x+2\right)+3\)\(=\left[-2x^2\left(x+2\right)-3x\left(x+2\right)+\left(x+2\right)\right]+3\)
\(=\left(x+2\right)\left(-2x^2-3x+1\right)+3\)
Làm tương tự như trên \(\Rightarrow x+2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Leftrightarrow x\in\left\{-5;-3;-1;1\right\}\)
Vậy...
d)\(f\left(x\right)=x^3-3x^2-4x+3=x\left(x^2-3x-4\right)+3=x\left(x+1\right)\left(x-4\right)+3\)
Làm tương tự như trên \(\Rightarrow x+1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow x\in\left\{-4;-2;0;2\right\}\)
Vậy...
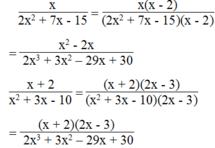
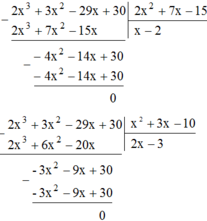
Chết mẹ nhầm; đề đây nha:
Tìm m sao cho với mọi x, ta có: 2x3−3x2+x+m=(x+2)(2x2 -7x+15)
Bài giải:
Cách 1: Ta có
(x+2)(2x2−7x+15)
=2x3−7x2+15x+4x2−14x+30
=2x3−3x2+x+30
Vì 2x3−3x2+x+m=2x3−3x2+x+30⇒m=30.
Cách 2: Cho x=−2 thì vế phải bằng 0. Khi đó vế trái bằng m−30. Do đó m = 30. Thử lại thấy thỏa mãn.