Cho tam giác ABC cân tại A đường trung tuyến BM.TRên cạnh BC lấy điểm D sao cho BD=2BC.C/M BM vuông góc với AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KB
17 tháng 2 2019
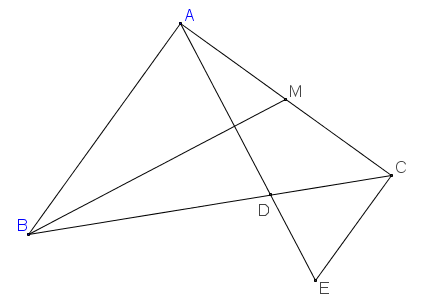
Gọi E là giao điểm của AD và đường thẳng đi qua C , vuông góc với CA
Do AB // CE ( GT ) \(\Rightarrow\dfrac{AB}{CE}=\dfrac{BD}{DC}=2\) ( Định lý Ta - lét )
Vì tam giác ABC cân tại A \(\Rightarrow AB=AC\)
Mà \(AC=2AM\) ( do BM là trung tuyến \(\Rightarrow AM=MC=\dfrac{1}{2}AC\))
\(\Rightarrow AB=2AM\)
\(\Rightarrow\dfrac{2AM}{CE}=2\Rightarrow\dfrac{AM}{CE}=1\Rightarrow AM=CE\)
Xét tam giác BAM và tam giác ACE có :
\(\left\{{}\begin{matrix}AB=AC\left(GT\right)\\\widehat{BAM}=\widehat{ACE}\left(=90^o\right)\\AM=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\) tam giác BAM = tam giác ACE ( c . g . c )
\(\Rightarrow\) góc AMB = góc AEC ( 2 góc t/ứng )
Mà góc AEC + góc CAE = 90 độ
=> góc AMB + góc CAE = 90 độ
=> BM vuông góc với AD ( đpcm )
D
11 tháng 5 2023
Để chứng minh điều này, ta có thể sử dụng các bước sau:
- Chứng minh tam giác BAD cân tại B (vì BD = BA) và tam giác BAN cân tại B (vì BM là phân giác của góc A).
- Chứng minh góc BAD = góc BAN (vì hai tam giác cân trên có hai góc ở đáy bằng nhau).
- Chứng minh góc HAD = góc NAD (vì AN vuông góc với BD).
- Chứng minh tam giác HAD đồng dạng với tam giác NAD (vì hai tam giác có hai góc bằng nhau).
- Chứng minh DH/DA = NA/ND (vì hai tam giác đồng dạng trên có tỉ số các cạnh tương ứng bằng nhau).
- Chứng minh DH/DA = AC/AB (vì NA/ND = AC/AB theo định lí Thales).
- Chứng minh DH song song với AC (vì hai đoạn thẳng có tỉ số các cạnh tương ứng bằng nhau).
Vậy ta đã chứng minh được DH song song với AC.
Kẻ đường thẳng qua C vuông góc AC cắt AD tại E
ta có ABCE=BDCD=2ABCE=BDCD=2 (1)
mà AB =AC =2 .AM (2)
từ (1, 2) =>AMCE=1AMCE=1 =>AM =CE
=>△BAM=△ACE△BAM=△ACE (c, g, c)
=>ABMˆ=CAEˆABM^=CAE^
mà ABMˆ+AMBˆ=90∘ABM^+AMB^=90∘
=>CAEˆ+AMBˆ=90∘CAE^+AMB^=90∘
=>BM vuông góc AD(đpcm)
Kẻ DE // BM \(\rightarrow\frac{IM}{DE}=\frac{3}{5},BM=3DE\rightarrow MB=5MI\)
\(AB=a\rightarrow AM=\frac{a}{2},BM^2=\frac{5a^2}{4}\rightarrow MI.MB=\frac{Mb^2}{5}=\frac{a^2}{4}\)
\(AM^2=\frac{a^2}{4}\rightarrow MA^2=MI.MB=\frac{MB^2}{5}=\frac{a^2}{4}\)