Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

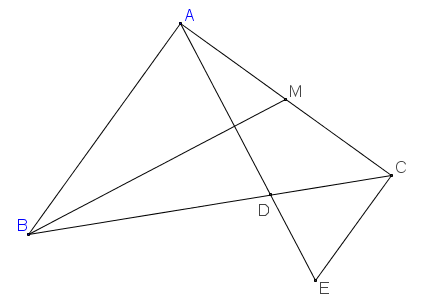
Gọi E là giao điểm của AD và đường thẳng đi qua C , vuông góc với CA
Do AB // CE ( GT ) \(\Rightarrow\dfrac{AB}{CE}=\dfrac{BD}{DC}=2\) ( Định lý Ta - lét )
Vì tam giác ABC cân tại A \(\Rightarrow AB=AC\)
Mà \(AC=2AM\) ( do BM là trung tuyến \(\Rightarrow AM=MC=\dfrac{1}{2}AC\))
\(\Rightarrow AB=2AM\)
\(\Rightarrow\dfrac{2AM}{CE}=2\Rightarrow\dfrac{AM}{CE}=1\Rightarrow AM=CE\)
Xét tam giác BAM và tam giác ACE có :
\(\left\{{}\begin{matrix}AB=AC\left(GT\right)\\\widehat{BAM}=\widehat{ACE}\left(=90^o\right)\\AM=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\) tam giác BAM = tam giác ACE ( c . g . c )
\(\Rightarrow\) góc AMB = góc AEC ( 2 góc t/ứng )
Mà góc AEC + góc CAE = 90 độ
=> góc AMB + góc CAE = 90 độ
=> BM vuông góc với AD ( đpcm )

Kẻ đường thẳng qua C vuông góc AC cắt AD tại E
ta có ABCE=BDCD=2ABCE=BDCD=2 (1)
mà AB =AC =2 .AM (2)
từ (1, 2) =>AMCE=1AMCE=1 =>AM =CE
=>△BAM=△ACE△BAM=△ACE (c, g, c)
=>ABMˆ=CAEˆABM^=CAE^
mà ABMˆ+AMBˆ=90∘ABM^+AMB^=90∘
=>CAEˆ+AMBˆ=90∘CAE^+AMB^=90∘
=>BM vuông góc AD(đpcm)
Kẻ DE // BM \(\rightarrow\frac{IM}{DE}=\frac{3}{5},BM=3DE\rightarrow MB=5MI\)
\(AB=a\rightarrow AM=\frac{a}{2},BM^2=\frac{5a^2}{4}\rightarrow MI.MB=\frac{Mb^2}{5}=\frac{a^2}{4}\)
\(AM^2=\frac{a^2}{4}\rightarrow MA^2=MI.MB=\frac{MB^2}{5}=\frac{a^2}{4}\)