được thì giải chi tiết hộ mình...
Đọc tiếp
được thì giải chi tiết hộ mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
1.
Nếu BC là đáy lớn \(\Rightarrow S_{MBC}=S_{MAB}+S_{ABCD}\Rightarrow S_{MBC}>S_{ABCD}\) (không thỏa mãn)
\(\Rightarrow BC\) là đáy nhỏ \(\Rightarrow S_{MAD}=S_{MBC}+S_{ABCD}=S_{MBC}+3S_{MBC}=4S_{MBC}\)
Từ M kẻ đường thẳng vuông góc AD và BC, lần lượt cắt BC tại H và AD tại K
\(\Rightarrow S_{MAD}=\dfrac{1}{2}MK.AD\) ; \(S_{MBC}=\dfrac{1}{2}MH.BC\)
\(\Rightarrow MK.AD=4MH.BC\Rightarrow\dfrac{AD}{BC}=4.\dfrac{MH}{KM}=4.\dfrac{AM}{BM}=4.\dfrac{BC}{AD}\) (theo Talet)
\(\Rightarrow AD^2=4BC^2\Rightarrow AD=2BC\Rightarrow\overrightarrow{AD}=2\overrightarrow{BC}\)
Ta có: \(\overrightarrow{BC}=\left(7;-1\right)\) ; \(\overrightarrow{AD}=\left(x_0+2;y_0+2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_0+2=14\\y_0+2=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=12\\y_0=-4\end{matrix}\right.\) \(\Rightarrow x_0-y_0=16\)
TK
22 tháng 8 2021
Để \(\sqrt{\dfrac{1}{3-2x}}\) có nghĩa
Khi\(\dfrac{1}{3-2x}\ge0\)
\(\Leftrightarrow3-2x>0\)
\(\Leftrightarrow-2x< -3\)
\(\Leftrightarrow x>\dfrac{3}{2}\)
HN
9 tháng 9 2017
Ta thấy rằng 39 x 3 = 117
Vậy số đó là:
117 - 25 = 92
Đ/S: 92
Bạn còn viết sai đề bài nên mình làm thế này
5 tháng 7 2021
b) \(\dfrac{3\pi}{2}< \alpha< 2\pi\)\(\Rightarrow cos\alpha>0;sin\alpha< 0\)
Có \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)\(\Rightarrow cos\alpha=\dfrac{4}{5}\)
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{3}{5}\)
\(sin\left(\alpha-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sin\alpha-cos\alpha\right)=\dfrac{\sqrt{2}}{2}\left(-\dfrac{3}{5}-\dfrac{4}{5}\right)=-\dfrac{7\sqrt{2}}{10}\)
Bài 2:
a) Gọi đt d vuông góc với đường thẳng \(\Delta\)có dạng: \(d:-4x+3y+c=0\)
\(A\in\left(d\right)\Rightarrow-4+3+c=0\Leftrightarrow c=1\)
Vậy \(d:-4x+3y+1=0\)
b) Gọi pt đường tròn (C) tâm A có dạng \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=R^2\)
Vì (C) tiếp xúc với \(\Delta\)
\(\Rightarrow\)\(R=d_{\left(A;\Delta\right)}=\dfrac{\left|3+4+5\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=\dfrac{144}{25}\)
Vậy...
18 tháng 3 2022
$a\big)$
$ZnO+H_2\xrightarrow{t^o}Zn+H_2O$
$CuO+H_2\xrightarrow{t^o}Cu+H_2O$
$b\big)$
$n_{H_2}=\frac{3,92}{22,4}=0,175(2)$
Theo PT: $n_{H_2O}=n_{H_2}=0,175(mol)$
$\to y=m_{H_2O}=0,175.18=3,15(g)$
BTKL:
$m_M+m_{H_2}=m_N+m_{H_2O}$
$\to m_N=14,1+0,175.2-3,15=11,3(g)$
$\to x=11,3(g)$
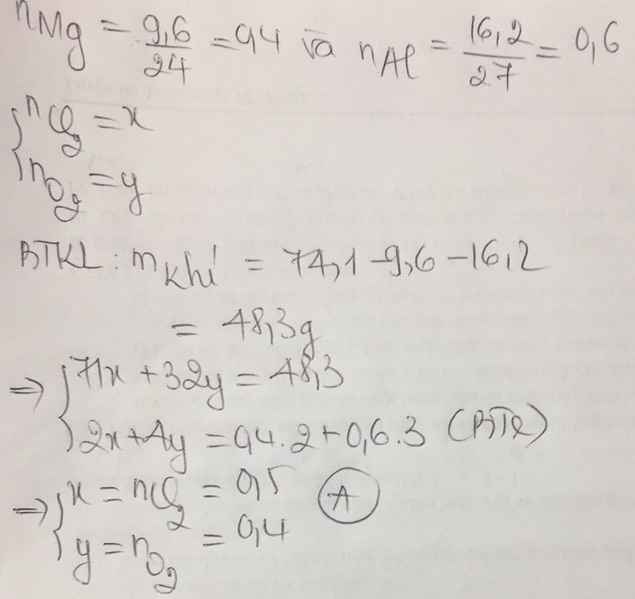
Gọi x, y lần lượt là số điện trở của R1 và R2.
Vì đoạn mạch mắc nối tiếp nên ta có: Rtđ = R1 + R2 + ... + Rn
từ đó ta có: 4x + 8y = 48
⇔ x + 2y = 12
⇒ x = 12 - 2y