
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) \(\dfrac{3\pi}{2}< \alpha< 2\pi\)\(\Rightarrow cos\alpha>0;sin\alpha< 0\)
Có \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)\(\Rightarrow cos\alpha=\dfrac{4}{5}\)
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{3}{5}\)
\(sin\left(\alpha-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sin\alpha-cos\alpha\right)=\dfrac{\sqrt{2}}{2}\left(-\dfrac{3}{5}-\dfrac{4}{5}\right)=-\dfrac{7\sqrt{2}}{10}\)
Bài 2:
a) Gọi đt d vuông góc với đường thẳng \(\Delta\)có dạng: \(d:-4x+3y+c=0\)
\(A\in\left(d\right)\Rightarrow-4+3+c=0\Leftrightarrow c=1\)
Vậy \(d:-4x+3y+1=0\)
b) Gọi pt đường tròn (C) tâm A có dạng \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=R^2\)
Vì (C) tiếp xúc với \(\Delta\)
\(\Rightarrow\)\(R=d_{\left(A;\Delta\right)}=\dfrac{\left|3+4+5\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=\dfrac{144}{25}\)
Vậy...


Pt đã cho có nghiệm duy nhất khi và chỉ khi:
\(m^2-4\ne0\Rightarrow m\ne\pm2\)
\(\Rightarrow\) Có \(5-\left(-5\right)+1-2=9\) giá trị nguyên của m

Đường thẳng \(\Delta:\left\{{}\begin{matrix}x=1+4t\\y=2-3t\end{matrix}\right.\) đi qua điểm \(A\left(1;2\right)\) và có VTCP \(\overrightarrow{u}=\left(4;-3\right)\)
\(\Rightarrow\overrightarrow{n}=\left(3;4\right)\) là VTPT của đường thẳng
\(\Rightarrow\) PT tổng quát: \(3\left(x-1\right)+4\left(y-2\right)=0\Leftrightarrow3x+4y-11=0\)
\(\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|3.1+4.\left(-1\right)-11\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)

ĐKXĐ: \(-1\le x\le4\)
\(\Leftrightarrow\left(x-3\right)\sqrt{1+x}-\left(x-3\right)+x-x\sqrt{4-x}=2x^2-6x\)
\(\Leftrightarrow\left(x-3\right)\left(\sqrt{1+x}-1\right)+x\left(1-\sqrt{4-x}\right)=2x^2-6x\)
\(\Leftrightarrow\dfrac{x\left(x-3\right)}{\sqrt{1+x}+1}+\dfrac{x\left(x-3\right)}{1+\sqrt{4-x}}=2\left(x^2-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x=0\Rightarrow x=...\\\dfrac{1}{\sqrt{1+x}+1}+\dfrac{1}{1+\sqrt{4-x}}=2\left(1\right)\end{matrix}\right.\)
Xét (1), do \(VT< \dfrac{1}{1}+\dfrac{1}{1}=2\Rightarrow VT< VP\Rightarrow\left(1\right)\) vô nghiệm
Vậy ...


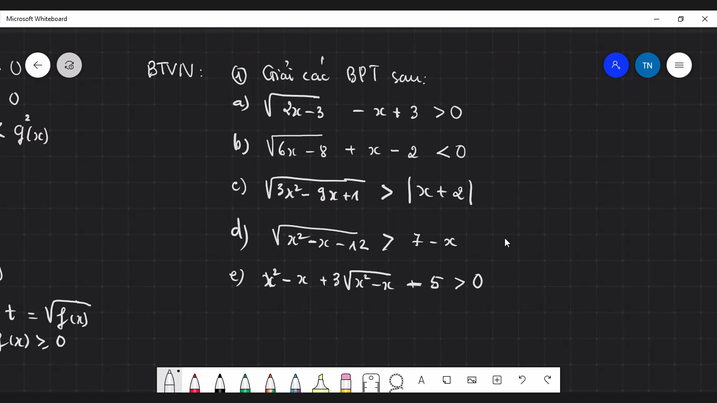



 iải chi tiết hộ em với
iải chi tiết hộ em với 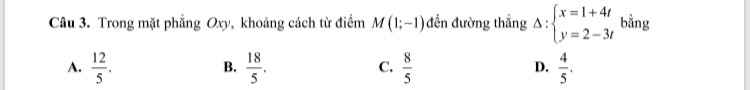
 Giải chi tiết hộ em với ạ
Giải chi tiết hộ em với ạ 
Em cần hỗ trợ như nào vậy em?
1.
Nếu BC là đáy lớn \(\Rightarrow S_{MBC}=S_{MAB}+S_{ABCD}\Rightarrow S_{MBC}>S_{ABCD}\) (không thỏa mãn)
\(\Rightarrow BC\) là đáy nhỏ \(\Rightarrow S_{MAD}=S_{MBC}+S_{ABCD}=S_{MBC}+3S_{MBC}=4S_{MBC}\)
Từ M kẻ đường thẳng vuông góc AD và BC, lần lượt cắt BC tại H và AD tại K
\(\Rightarrow S_{MAD}=\dfrac{1}{2}MK.AD\) ; \(S_{MBC}=\dfrac{1}{2}MH.BC\)
\(\Rightarrow MK.AD=4MH.BC\Rightarrow\dfrac{AD}{BC}=4.\dfrac{MH}{KM}=4.\dfrac{AM}{BM}=4.\dfrac{BC}{AD}\) (theo Talet)
\(\Rightarrow AD^2=4BC^2\Rightarrow AD=2BC\Rightarrow\overrightarrow{AD}=2\overrightarrow{BC}\)
Ta có: \(\overrightarrow{BC}=\left(7;-1\right)\) ; \(\overrightarrow{AD}=\left(x_0+2;y_0+2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_0+2=14\\y_0+2=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=12\\y_0=-4\end{matrix}\right.\) \(\Rightarrow x_0-y_0=16\)