Cho tam giác ABC vuông tại A (AB<AC);D,E lần lượt là trung điểm của BC,AC.Lấy F đối xứng với E qua D,kẻ AH vuông góc vớiBC , M là trung điểm của CHa)c/m tứ giác BECF là HBHb)c/m tứ giác AEFB là HCNc)c/m AM vuông góc với MFd)Tính diện tích tứ giác MFBE biếtAB=6cm;AC=8cmGIÚP EM VỚI Ạ :3 CẦN CÂU D VƠI CÂU C :3 ai có tâm làm 3 câu cũng đc ạ :3333 CẢM ƠN :333 ...
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC);D,E lần lượt là trung điểm của BC,AC.Lấy F đối xứng với E qua D,kẻ AH vuông góc vớiBC , M là trung điểm của CH
a)c/m tứ giác BECF là HBH
b)c/m tứ giác AEFB là HCN
c)c/m AM vuông góc với MF
d)Tính diện tích tứ giác MFBE biết
AB=6cm;AC=8cm
GIÚP EM VỚI Ạ :3 CẦN CÂU D VƠI CÂU C :3 ai có tâm làm 3 câu cũng đc ạ :3333 CẢM ƠN :333
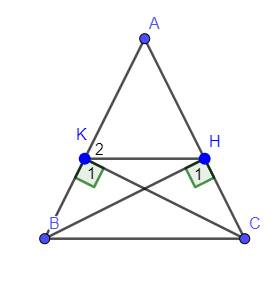
c) Gọi O là giao điểm của BE và AF
Xét tam giác AHC có: M là TĐ của HC(gt) , E là TĐ của AC (gt)
\(\Rightarrow ME\)là đường trung bình của tam giác AHC
\(\Rightarrow ME//AH\left(tc\right)\)
Mà \(AH\perp BC\)
\(\Rightarrow ME\perp BC\)
\(\Rightarrow\widehat{BME}=90^0\)
Vì ABFE là hcn (cmt)
\(\Rightarrow BE\)cắt AF tại TĐ mỗi đường (tc) mà O là giao điểm của BE và AF(c.vẽ)
\(\Rightarrow O\)là TĐ của BE và AF
Xét tam giác \(BME\)vuông tại M có đường trung tuyến OM ứng với cạnh huyền BE
\(\Rightarrow OM=\frac{1}{2}BE\left(tc\right)\)
Mà \(BE=AF\)(tc hcn)
\(\Rightarrow OM=\frac{1}{2}AF\)
Xét tam giác AMF có trung tuyến OM ứng với cạnh AF và \(OM=\frac{1}{2}AF\left(cmt\right)\)
\(\Rightarrow\Delta AMF\)vuông tại M
\(\Rightarrow\widehat{FMA}=90^0\)
\(\Rightarrow AM\perp FM\)