Question

[Bạch Khánh Linh]

1. Cho ΔABC. Các tia phân giác của các góc B và C cắt nhau tại O. Chứng minh rằng OA là tia phân giác của góc A

Hướng dẫn : Từ O kẻ các dường vuông góc với cạnh của tam giác ABC

2. Cho tam giác ABC có AB < AC .Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IE vuông góc với đường thẳng AB, kẻ IF vuông góc với đường thẳng AC.Chứng minh BE =CF

Answer 1

[Vũ Minh Tuấn]

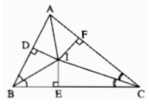
Hình bạn tự vẽ nha!

Bài 2:

Gọi \(IM\) là đường trung trực của \(BC.\)

\(\Rightarrow\left\{{}\begin{matrix}BM=CM\\IM\perp BC\end{matrix}\right.\) (định nghĩa đường trung trực).

Xét 2 \(\Delta\) vuông \(BMI\) và \(CMI\) có:

\(\widehat{BMI}=\widehat{CMI}=90^0\) (vì \(IM\perp BC\))

\(BM=CM\left(cmt\right)\)

Cạnh MI chung

=> \(\Delta BMI=\Delta CMI\) (2 cạnh góc vuông tương ứng bằng nhau).

=> \(BI=CI\) (2 cạnh tương ứng).

Xét 2 \(\Delta\) vuông \(AEI\) và \(AFI\) có:

\(\widehat{AEI}=\widehat{AFI}=90^0\left(gt\right)\)

Cạnh AI chung

\(\widehat{EAI}=\widehat{FAI}\) (vì \(AI\) là tia phân giác của \(\widehat{A}\))

=> \(\Delta AEI=\Delta AFI\) (cạnh huyền - góc nhọn).

=> \(EI=FI\) (2 cạnh tương ứng).

Xét 2 \(\Delta\) vuông \(BEI\) và \(CFI\) có:

\(\widehat{BEI}=\widehat{CFI}=90^0\)

\(BI=CI\left(cmt\right)\)

\(EI=FI\left(cmt\right)\)

=> \(\Delta BEI=\Delta CFI\) (cạnh huyền - cạnh góc vuông).

=> \(BE=CF\) (2 cạnh tương ứng) (đpcm).

Chúc bạn học tốt!

Answer 2

[Bạch Khánh Linh]

bạn làm bài 1 hộ mình đi