một nhà máy sản xuất kẹo đựng kẹo trong hộp hình quả trứng cao 8cm. Gọi trục của hộp kẹo là đường thẳng đi qua hai đỉnh của quả trứng. Thiết diện tạo bởi mặt phẳng vuông góc với trục và cách đều hai đỉnh là một dường tròn bán kính 2cm. Mặt phẳng đi qua trục cắt mặt xung quanh của một hộp kẹo là một đường elip. Hỏi hộp có thể đựng được tối đa bao nhiêu cái kẹo biết thể tích mỗi cái kẹo là 1 cm3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
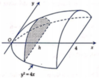
Gọi thiết diện mặt cắt là hình vuông ABCD.
Xét mặt đáy tâm O như hình vẽ. Vì thiết diện qua trục là hình vuông cạnh 2a nên chiều cao của hình trụ OO' = 2a = BC và OA = a.
⇒ A B = 2 O A 2 - O M 2 = a 3
Diện tích thiết diện cần tính: A B . C D = 2 a 2 3 .

Đáp án A
Xét thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm x là nửa elip có bán trục lớn bằng 2 x , do đó có bán trục nhỏ bằng x (do trục lớn gấp đôi trục nhỏ)
Suy ra diện tích của thiết diện tại điểm x là S x = 1 2 . π .2 x . x = π x
Vậy thiết diện của vật thể là V = ∫ 0 4 π x d x = π x 2 2 4 0 = 8 π . Chọn đáp án A

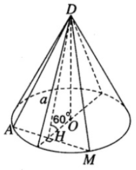
Xét mặt phẳng (DAM) đi qua đỉnh D tạo với mặt phẳng đáy một góc 600, cắt đường tròn đáy tại hai điểm A và M. Từ tâm O của đường tròn đáy ta vẽ OH ⊥ AM, do vậy H là trung điểm của đoạn AM. Ta có AM ⊥ (DOH) vì AM ⊥ OH và AM ⊥ DO.
Vậy
∠
DHO = 60
°
và 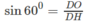
hay 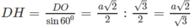
Gọi SΔ DAM là diện tích thiết diện cần tìm, ta có: S △ DAM = AH.DH
Mà ![]()
![]()
Vậy
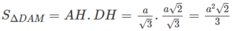

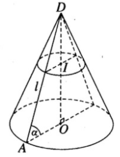
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với 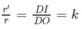
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
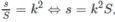
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α