Tam giác ABC cân ở A(A<90), kẻ BD vuông góc vs AC ở D, CE vuông góc vs AB ở E
a) Chứng minh tam giác ADE cân
b) Chứng minh DE//BC
c)Gọi I là gđ của BD, EC. Chứng minh IB=IC
d) Chứng minh AI vuông góc vs BC
AI là phân giác góc A
e) Chứng minh AI đi qua trung điểm BC
Không cần vẽ hình nha. Giúp mink nhé. Mink cảm mơn

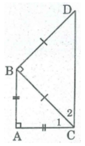
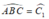
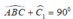 ( tính chất tam giác vuông).
( tính chất tam giác vuông).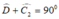
a) \(\Delta BEC\)và \(\Delta CDB\)có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
\(\widehat{BEC}=\widehat{BDC}=90^0\)
\(\Delta BEC=\Delta CDB\left(g-c-g\right)\)
\(\Rightarrow BE=CD\). Mặt khác AB=CD (gt) nên ta có AE=AD\(\Rightarrow\Delta AED\)cân tại A
b) \(\Delta AED\)cân tại A \(\Rightarrow\widehat{AED}=\frac{180^0-\widehat{EAD}}{2}\left(1\right)\)
\(\Delta ABC\)cân tại A \(\Rightarrow\widehat{EBC}=\frac{180^0-\widehat{EAD}}{2}\left(2\right)\)
Từ (1) và(2) ta có \(\widehat{AED}=\widehat{EBC}\)mà 2 góc ở vị trí đồng vị nên \(DE//BC\)
c) \(\Delta DEB\)và \(\Delta EDC\)có
DE chung
BE=DC(cmt)
BD=CE (\(\Delta BEC=\Delta CDB\))
\(\Delta DEB=\Delta EDC\left(c-c-c\right)\) \(\Rightarrow\widehat{EBD}=\widehat{DCE}\)
Mặt khác \(\widehat{ABC}=\widehat{ACB}\)\(\Rightarrow\widehat{IBC}=\widehat{ICB}\Rightarrow\Delta IBC\)cân tại I nên IB=IC