Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

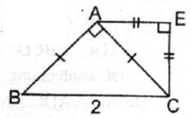
∠ E = ∠ (ECB) = 90 0 , ∠ B = 45 0
∠ B + ∠ (EAB) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (EAB) = 180 0 - ∠ B = 180 0 – 45 0 = 135 0
Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:
A B 2 + A C 2 = B C 2 mà AB = AC (gt)
⇒ 2 A B 2 = B C 2 = 2 2 = 4
A B 2 = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)
Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:
E A 2 + E C 2 = A C 2 , mà EA = EC (gt)
⇒ 2 E A 2 = A C 2 = 2
E A 2 = 1
⇒ EA = 1(cm) ⇒ EC = 1(cm)

Lời giải:
a. $BAC$ là tam giác vuông cân tại $A$
$\Rightarrow \widehat{BCA}=45^0$
$ACE$ là tam giác vuông cân tại $E$
$\Rightarrow \widehat{EAC}=45^0$
Do đó: $\widehat{BCA}=\widehat{EAC}$. Mà 2 góc này ở vị trí so le trong nên $AE\parallel BC$. Mà $\widehat{E}=90^0$ nên $AECB$ là hình thang vuông.
-----------------
Tính góc:
Hình thang vuông $AECB$ có $\widehat{E}=90^0$ đương nhiên $\widehat{C}=180^0-\widehat{E}=90^0$
$\widehat{ABC}=45^0$ (do $ABC$ vuông cân tại $A$)
$\widehat{BAE}=\widehhat{BAC}+\widehat{EAC}=90^0+45^0=135^0$
Tính cạnh:
Vì $ABC$ vuông cân tại $A$ nên $AB=AC$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2=4$
$AB^2+AB^2=4$
$2AB^2=4\Rightarrow AB=\sqrt{2}$ (cm)
$\Rightarrow AC=\sqrt{2}$ (cm)
Áp dụng định lý Pitago cho tam giác $ACE$ vuông cân tại $E$:
$AE^2+EC^2=AC^2=2$
$2AE^2=2\Rightarrow AE=1$ (cm)
$EC=AE=1$ (cm)
Vậy.........

Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông

Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.
b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.
Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.
b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.

a) Ta có : ACB = 45° ( ∆ABC vuông cân tại A )
Ta có : AEC = 45° ( ∆ACE vuông cân tại E )
=> ACB = AEC = 45°
Mà 2 góc này ở vị trí so le trong
=> AE//BC
=> AEBC là hình thang
Mà AEC = 90°
=> AEBC là hình thang vuông